RD Sharma Solutions for Class 10 Maths Chapter 5 Trigonometric Ratios Exercise 5.1

The science of measuring triangles is trigonometry. In other words, it deals with the measurement of the sides and angles of triangles. This exercise contains problems dealing with finding all the trigonometric ratios when one of them is given. Further, the value of an expression is also asked to be evaluated. All the solutions to this and other chapters are easily available on the RD Sharma Solutions Class 10. For specific doubts regarding the solution and concept, students can download RD Sharma Solutions for Class 10 Maths Chapter 5 Trigonometric Ratios Exercise 5.1 PDF below.

RD Sharma Solutions for Class 10 Maths Chapter 5 Trigonometric Ratios Exercise 5.1

Download PDF

carouselExampleControls111

Previous



Next

Access RD Sharma Solutions for Class 10 Maths Chapter 5 Trigonometric Ratios Exercise 5.1

1. In each of the following, one of the six trigonometric ratios s given. Find the values of the other trigonometric ratios.

(i) sin A = 2/3

Solution:

We have,

sin A = 2/3 ……..….. (1)

As we know, by sin definition,

sin A =  Perpendicular/ Hypotenuse = 2/3 ….(2)

By comparing eq. (1) and (2), we have

Opposite side = 2 and Hypotenuse = 3

Now, on using Pythagoras’ theorem in Δ ABC,

AC² = AB^{2 +} BC²

Putting the values of the perpendicular side (BC) and hypotenuse (AC) and for the base side as (AB), we get

⇒ 3² = AB² + 2²

AB² = 3² – 2²

AB² = 9 – 4

AB^{2 =} 5

AB = √5

Hence, Base = √5

By definition,

cos A = Base/Hypotenuse

⇒ cos A = √5/3

Since, cosec A = 1/sin A = Hypotenuse/Perpendicular

⇒ cosec A = 3/2

And, sec A = Hypotenuse/Base

⇒ sec A = 3/√5

And, tan A = Perpendicular/Base

⇒ tan A =  2/√5

And, cot A = 1/ tan A = Base/Perpendicular

⇒ cot A = √5/2

(ii) cos A = 4/5

Solution:

We have,

cos A = 4/5 …….…. (1)

As we know, by cos definition,

cos A = Base/Hypotenuse …. (2)

By comparing eq. (1) and (2), we get

Base = 4 and Hypotenuse = 5

Now, using Pythagoras’ theorem in Δ ABC,

AC² = AB² + BC²

Putting the value of base (AB) and hypotenuse (AC) and for the perpendicular (BC), we get

5² = 4² + BC²

BC² = 5² – 4²

BC² = 25 – 16

BC² = 9

BC= 3

Hence, Perpendicular = 3

By definition,

sin A = Perpendicular/Hypotenuse

⇒ sin A = 3/5

Then, cosec A = 1/sin A

⇒ cosec A= 1/ (3/5) = 5/3 = Hypotenuse/Perpendicular

And, sec A = 1/cos A

⇒ sec A =Hypotenuse/Base

sec A = 5/4

And, tan A = Perpendicular/Base

⇒ tan A = 3/4

Next, cot A = 1/tan A = Base/Perpendicular

∴ cot A = 4/3

(iii) tan θ = 11/1

Solution:

We have, tan θ = 11…..…. (1)

By definition,

tan θ = Perpendicular/ Base…. (2)

On Comparing eq. (1) and (2), we get;

Base = 1 and Perpendicular = 5

Now, using Pythagoras’ theorem in Δ ABC,

AC² = AB² + BC²

Putting the value of base (AB) and perpendicular (BC) to get hypotenuse(AC), we get

AC² = 1² + 11²

AC² = 1 + 121

AC²= 122

AC= √122

Hence, hypotenuse = √122

By definition,

sin = Perpendicular/Hypotenuse

⇒ sin θ = 11/√122

And, cosec θ = 1/sin θ

⇒ cosec θ = √122/11

Next, cos θ = Base/ Hypotenuse

⇒ cos θ = 1/√122

And, sec θ = 1/cos θ

⇒ sec θ = √122/1 = √122

And, cot θ  = 1/tan θ

∴ cot θ = 1/11

(iv) sin θ = 11/15

Solution:

We have,  sin θ = 11/15 ………. (1)

By definition,

sin θ = Perpendicular/ Hypotenuse …. (2)

On Comparing eq. (1) and (2), we get,

Perpendicular = 11 and Hypotenuse= 15

Now, using Pythagoras’ theorem in Δ ABC,

AC² = AB² + BC²

Putting the value of perpendicular (BC) and hypotenuse (AC) to get the base (AB), we have

15² = AB² +11²

AB² = 15² – 11²

AB² = 225 – 121

AB² = 104

AB = √104

AB= √ (2×2×2×13)

AB= 2√(2×13)

AB= 2√26

Hence, Base = 2√26

By definition,

cos θ = Base/Hypotenuse

∴ cosθ = 2√26/ 15

And, cosec θ = 1/sin θ

∴ cosec θ = 15/11

And, secθ = Hypotenuse/Base

∴ secθ =15/ 2√26

And,  tan θ = Perpendicular/Base

∴ tanθ =11/ 2√26

And,  cot θ = Base/Perpendicular

∴ cotθ =2√26/ 11

 (v) tan α = 5/12

Solution:

We have,  tan α = 5/12 …. (1)

By definition,

tan α = Perpendicular/Base…. (2)

On Comparing eq. (1) and (2), we get

Base = 12 and Perpendicular side = 5

Now, using Pythagoras’ theorem in Δ ABC

AC² = AB² + BC²

Putting the value of the base (AB) and the perpendicular (BC) to get hypotenuse (AC), we have

AC² = 12² + 5²

AC² = 144 + 25

AC²= 169

AC = 13 [After taking sq root on both sides]

Hence, Hypotenuse = 13

By definition,

sin α  = Perpendicular/Hypotenuse

∴ sin α = 5/13

And, cosec α  = Hypotenuse/Perpendicular

∴ cosec α = 13/5

And,  cos α = Base/Hypotenuse

∴ cos α = 12/13

And,  sec α =1/cos α

∴ sec α = 13/12

And, tan α = sin α/cos α

∴ tan α=5/12

Since, cot α = 1/tan α

∴ cot α =12/5

 (vi) sin θ = √3/2

Solution:

We have, sin θ = √3/2 …………. (1)

By definition,

sin θ = Perpendicular/ Hypotenuse….(2)

On Comparing eq. (1) and (2), we get;

Perpendicular = √3 and Hypotenuse = 2

Now, using Pythagoras’ theorem in Δ ABC,

AC² = AB² + BC²

Putting the value of perpendicular (BC) and hypotenuse (AC) and getting the base (AB), we get

2² = AB² + (√3)²

AB² = 2² – (√3)²

AB² = 4 – 3

AB² = 1

AB = 1

Thus, Base = 1

By definition,

cos θ = Base/Hypotenuse

∴ cos θ = 1/2

And, cosec θ = 1/sin θ

Or cosec θ= Hypotenuse/Perpendicular

∴ cosec θ =2/√3

And,  sec θ = Hypotenuse/Base

∴ sec θ = 2/1

And,  tan θ = Perpendicular/Base

∴ tan θ = √3/1

And,  cot θ = Base/Perpendicular

∴ cot θ = 1/√3

(vii) cos θ = 7/25

Solution:

We have, cos θ = 7/25 ……….. (1)

By definition,

cos θ = Base/Hypotenuse

On Comparing eq. (1) and (2), we get

Base = 7 and Hypotenuse = 25

Now, using Pythagoras’ theorem in Δ ABC,

AC²= AB² + BC²

Putting the value of base (AB) and hypotenuse (AC) to get the perpendicular (BC),

25² = 7² +BC²

BC² = 25² – 7²

BC² = 625 – 49

BC² = 576

BC= √576

BC= 24

Hence, the Perpendicular side = 24

By definition,

sin θ = perpendicular/Hypotenuse

∴ sin θ = 24/25

Since, cosec θ = 1/sin θ

Also, cosec θ= Hypotenuse/Perpendicular

∴ cosec θ = 25/24

Since,  sec θ = 1/cosec θ

Also,  sec θ = Hypotenuse/Base

∴ sec θ = 25/7

Since,  tan θ = Perpendicular/Base

∴ tan θ = 24/7

Now,  cot = 1/tan θ

So,  cot θ = Base/Perpendicular

∴ cot θ = 7/24

(viii) tan θ = 8/15

Solution:

We have, tan θ = 8/15 …………. (1)

By definition,

tan θ = Perpendicular/Base …. (2)

On Comparing eq. (1) and (2), we get;

Base = 15 and Perpendicular = 8

Now, using Pythagoras’ theorem in Δ ABC,

AC² = 15² + 8²

AC² = 225 + 64

AC² = 289

AC = √289

AC = 17

Hence, Hypotenuse = 17

By definition,

Since,  sin θ = perpendicular/Hypotenuse

∴ sin θ = 8/17

Since, cosec θ = 1/sin θ

Also, cosec θ = Hypotenuse/Perpendicular

∴ cosec θ = 17/8

Since,  cos θ = Base/Hypotenuse

∴ cos θ = 15/17

Since,  sec θ = 1/cos θ

Also,  sec θ = Hypotenuse/Base

∴ sec θ = 17/15

Since, cot θ = 1/tan θ

Also,  cot θ = Base/Perpendicular

∴ cot θ = 15/8

(ix) cot θ = 12/5

Solution:

We have, cot θ = 12/5 …………. (1)

By definition,

cot θ = 1/tan θ

cot θ = Base/Perpendicular ……. (2)

On Comparing eq. (1) and (2), we have

Base = 12 and Perpendicular side = 5

Now, using Pythagoras’ theorem in Δ ABC,

AC²= AB² + BC²

Putting the value of base (AB) and perpendicular (BC) to get the hypotenuse (AC),

AC² = 12² + 5²

AC²= 144 + 25

AC² = 169

AC = √169

AC = 13

Hence, Hypotenuse = 13

By definition,

Since,  sin θ = perpendicular/Hypotenuse

∴ sin θ= 5/13

Since, cosec θ = 1/sin θ

Also, cosec θ= Hypotenuse/Perpendicular

∴ cosec θ = 13/5

Since,  cos θ = Base/Hypotenuse

∴ cos θ = 12/13

Since,  sec θ = 1/cosθ

Also,  sec θ = Hypotenuse/Base

∴ sec θ = 13/12

Since,  tanθ = 1/cot θ

Also,  tan θ = Perpendicular/Base

∴ tan θ = 5/12

(x)  sec θ = 13/5

Solution:

We have, sec θ = 13/5…….… (1)

By definition,

sec θ = Hypotenuse/Base…………. (2)

On Comparing eq. (1) and (2), we get

Base = 5 and Hypotenuse = 13

Now, using Pythagoras’ theorem in Δ ABC,

AC² = AB² + BC²

And putting the value of the base side (AB) and hypotenuse (AC) to get the perpendicular side (BC),

13² = 5² + BC²

BC² = 13² – 5²

BC²=169 – 25

BC²= 144

BC= √144

BC = 12

Hence, Perpendicular = 12

By definition,

Since,  sin θ = perpendicular/Hypotenuse

∴ sin θ= 12/13

Since, cosec θ= 1/ sin θ

Also, cosec θ= Hypotenuse/Perpendicular

∴ cosec θ = 13/12

Since cos θ= 1/sec θ

Also,  cos θ = Base/Hypotenuse

∴ cos θ = 5/13

Since,  tan θ = Perpendicular/Base

∴ tan θ = 12/5

Since,  cot θ = 1/tan θ

Also,  cot θ = Base/Perpendicular

∴ cot θ = 5/12

(xi)  cosec θ = √10

Solution:

We have, cosec θ = √10/1   ……..… (1)

By definition,

cosec θ = Hypotenuse/ Perpendicular …….….(2)

And, cosecθ = 1/sin θ

On comparing eq.(1) and(2), we get

Perpendicular side = 1 and Hypotenuse = √10

Now, using Pythagoras’ theorem in Δ ABC,

AC² = AB² + BC²

Putting the value of perpendicular (BC) and hypotenuse (AC) to get the base side (AB),

(√10)² = AB² + 1²

AB²= (√10)² – 1²

AB²= 10 – 1

AB = √9

AB = 3

So, Base side = 3

By definition,

Since,  sin θ = Perpendicular/Hypotenuse

∴ sin θ = 1/√10

Since,  cos θ = Base/Hypotenuse

∴ cos θ = 3/√10

Since,  sec θ = 1/cos θ

Also, sec θ = Hypotenuse/Base

∴ sec θ = √10/3

Since,  tan θ = Perpendicular/Base

∴ tan θ = 1/3

Since,  cot θ = 1/tan θ

∴ cot θ = 3/1

(xii)  cos θ =12/15

Solution:

We have; cos θ = 12/15 ………. (1)

By definition,

cos θ = Base/Hypotenuse……… (2)

By comparing eq. (1) and (2), we get

Base =12 and Hypotenuse = 15

Now, using Pythagoras’ theorem in Δ ABC, we get

AC² = AB²+ BC²

Putting the value of base (AB) and hypotenuse (AC) to get the perpendicular (BC),

15² = 12² + BC²

BC² = 15² – 12²

BC² = 225 – 144

BC ²= 81

BC = √81

BC = 9

So, Perpendicular = 9

By definition,

Since,  sin θ = perpendicular/Hypotenuse

∴ sin θ = 9/15 = 3/5

Since, cosec θ = 1/sin θ

Also, cosec θ = Hypotenuse/Perpendicular

∴ cosec θ= 15/9 = 5/3

Since,  sec θ = 1/cos θ

Also,  sec θ = Hypotenuse/Base

∴ sec θ = 15/12 = 5/4

Since,  tan θ = Perpendicular/Base

∴ tan θ = 9/12 = 3/4

Since,  cot θ = 1/tan θ

Also,  cot θ = Base/Perpendicular

∴ cot θ = 12/9 = 4/3

2. In a △ ABC, right angled at B, AB = 24 cm , BC = 7 cm. Determine

(i) sin A , cos A (ii) sin C, cos C

Solution:

(i) Given: In △ABC, AB = 24 cm, BC = 7cm and ∠ABC = 90^o

To find: sin A, cos A

By using Pythagoras’ theorem in △ABC, we have

AC² = AB² + BC²

AC² = 24² + 7²

AC² = 576 + 49

AC²= 625

AC = √625

AC= 25

Hence, Hypotenuse = 25

By definition,

sin A = Perpendicular side opposite to angle A/ Hypotenuse

sin A = BC/ AC

sin A = 7/ 25

And,

cos A = Base side adjacent to angle A/Hypotenuse

cos A = AB/ AC

cos A = 24/ 25

(ii) Given: In △ABC , AB = 24 cm and BC = 7cm and ∠ABC = 90^o

To find: sin C, cos C

By using Pythagoras’ theorem in △ABC, we have

AC² = AB² + BC²

AC² = 24² + 7²

AC² = 576 + 49

AC²= 625

AC = √625

AC= 25

Hence, Hypotenuse = 25

By definition,

sin C = Perpendicular side opposite to angle C/Hypotenuse

sin C = AB/ AC

sin C = 24/ 25

And,

cos C = Base side adjacent to angle C/Hypotenuse

cos A = BC/AC

cos A = 7/25

3. In fig. 5.37, find tan P and cot R. Is tan P = cot R? 

Solution:

By using Pythagoras’ theorem in △PQR, we have

PR² = PQ² + QR²

Putting the length of the given side PR and PQ in the above equation,

13² = 12² + QR²

QR² = 13² – 12²

QR² = 169 – 144

QR² = 25

QR = √25 = 5

By definition,

tan P = Perpendicular side opposite to P/ Base side adjacent to angle P

tan P = QR/PQ

tan P = 5/12 ………. (1)

And,

cot R= Base/Perpendicular

cot R= QR/PQ

cot R= 5/12 …. (2)

When comparing equations (1) and (2), we can see that the R.H.S. of both equations is equal.

Therefore, the L.H.S of both equations should also be equal.

∴ tan P = cot R

Yes, tan P = cot R = 5/12

4. If sin A = 9/41, compute cos A and tan A.

Solution:

Given that, sin A = 9/41 …………. (1)

Required to find: cos A, tan A

By definition, we know that

sin A = Perpendicular/ Hypotenuse……………(2)

On Comparing eq. (1) and (2), we get;

Perpendicular side = 9 and Hypotenuse = 41

Let’s construct △ABC as shown below,

And, here, the length of base AB is unknown.

Thus, by using Pythagoras’ theorem in △ABC, we get

AC² = AB² + BC²

41² = AB² + 9²

AB² = 41² – 9²

AB² = 168 – 81

AB= 1600

AB = √1600

AB = 40

⇒ Base of triangle ABC, AB = 40

We know that,

cos A = Base/ Hypotenuse

cos A =AB/AC

cos A =40/41

And,

tan A = Perpendicular/ Base

tan A = BC/AB

tan A = 9/40

5.  Given 15cot A= 8, find sin A and sec A.

Solution

We have, 15cot A = 8

Required to find: sin A and sec A

As 15 cot A = 8

⇒ cot A = 8/15 …….(1)

And we know,

cot A = 1/tan A

Also, by definition,

Cot A = Base side adjacent to ∠A/ Perpendicular side opposite to ∠A …. (2)

On comparing equations (1) and (2), we get

The base side adjacent to ∠A = 8

The perpendicular side opposite to ∠A = 15

So, by using Pythagoras’ theorem to △ABC, we have

AC² = AB² +BC²

Substituting values for sides from the figure,

AC² = 8² + 15²

AC² = 64 + 225

AC² = 289

AC = √289

AC = 17

Therefore, hypotenuse =17

By definition,

sin A = Perpendicular/Hypotenuse

⇒ sin A= BC/AC

sin A= 15/17 (using values from the above)

Also,

sec A= 1/ cos A

⇒ secA = Hypotenuse/ Base side adjacent to ∠A

∴ sec A= 17/8

 6. In △PQR, right-angled at Q, PQ = 4cm and RQ = 3 cm. Find the value of sin P, sin R, sec P and sec R.

Solution:

Given:

△PQR is right-angled at Q.

PQ = 4cm

RQ = 3cm

Required to find: sin P, sin R, sec P, sec R

Given △PQR,

By using Pythagoras’ theorem to △PQR, we get

PR² = PQ² +RQ²

Substituting the respective values,

PR² = 4² +3²

PR² = 16 + 9

PR² = 25

PR = √25

PR = 5

⇒ Hypotenuse =5

By definition,

sin P = Perpendicular side opposite to angle P/ Hypotenuse

sin P = RQ/ PR

⇒ sin P = 3/5

And,

sin R = Perpendicular side opposite to angle R/ Hypotenuse

sin R = PQ/ PR

⇒ sin R = 4/5

And,

sec P=1/cos P

secP = Hypotenuse/ Base side adjacent to ∠P

sec P = PR/ PQ

⇒ sec P = 5/4

Now,

sec R = 1/cos R

secR = Hypotenuse/ Base side adjacent to ∠R

sec R = PR/ RQ

⇒ sec R = 5/3

7. If cot θ = 7/8, evaluate

    (i)   (1+sin θ)(1–sin θ)/ (1+cos θ)(1–cos θ)

    (ii)  cot² θ

Solution:

(i) Required to evaluate:
, given = cot θ = 7/8

Taking the numerator, we have

(1+sin θ)(1–sin θ) = 1 – sin² θ [Since, (a+b)(a-b) = a² – b²]

Similarly,

(1+cos θ)(1–cos θ) = 1 – cos² θ

We know that,

sin² θ + cos² θ = 1

⇒ 1 – cos² θ = sin² θ

And,

1 – sin² θ = cos² θ

Thus,

(1+sin θ)(1 –sin θ) = 1 – sin² θ = cos² θ

(1+cos θ)(1–cos θ) = 1 – cos² θ = sin² θ

⇒

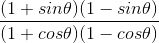
= cos² θ/ sin² θ

= (cos θ/sin θ)²

And, we know that (cos θ/sin θ) = cot θ

⇒

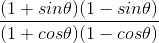
= (cot θ)²

= (7/8)²

= 49/ 64

(ii) Given,

cot θ = 7/8

So, by squaring on both sides, we get

(cot θ)² = (7/8)²

∴ cot θ² = 49/64

8. If 3cot A = 4, check whether (1–tan²A)/(1+tan²A) = (cos²A – sin²A) or not.

Solution:

Given,

3cot A = 4

⇒ cot A = 4/3

By definition,

tan A = 1/ Cot A = 1/ (4/3)

⇒ tan A = 3/4

Thus,

The base side adjacent to ∠A = 4

The perpendicular side opposite to ∠A = 3

In ΔABC, Hypotenuse is unknown.

Thus, by applying Pythagoras’ theorem in ΔABC,

We get

AC² = AB² + BC²

AC² = 4² + 3²

AC² = 16 + 9

AC² = 25

AC = √25

AC = 5

Hence, hypotenuse = 5

Now, we can find that

sin A = opposite side to ∠A/ Hypotenuse = 3/5

And,

cos A = adjacent side to ∠A/ Hypotenuse = 4/5

Taking the LHS,

Thus, LHS = 7/25

Now, taking RHS

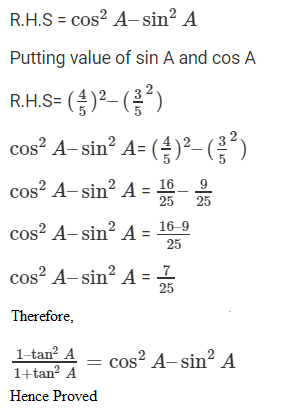
9. If tan θ = a/b, find the value of (cos θ + sin θ)/ (cos θ – sin θ)

Solution:

Given,

tan θ = a/b

And we know by definition that

tan θ = opposite side/ adjacent side

Thus, by comparison

Opposite side = a and adjacent side = b

To find the hypotenuse, we know that by Pythagoras’ theorem that

Hypotenuse² = opposite side² + adjacent side²

⇒ Hypotenuse = √(a² + b²)

So, by definition

sin θ = opposite side/ Hypotenuse

sin θ = a/ √(a² + b²)

And,

cos θ = adjacent side/ Hypotenuse

cos θ = b/ √(a² + b²)

Now,

After substituting for cos θ and sin θ, we have

∴

Hence Proved.

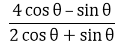
10. If 3 tan θ = 4, find the value of

Solution:

Given, 3 tan θ = 4

⇒ tan θ = 4/3

From, let’s divide the numerator and denominator by cos θ.

We get,

(4 – tan θ) / (2 + tan θ)

⇒ (4 – (4/3)) / (2 + (4/3)) [using the value of tan θ]

⇒ (12 – 4) / (6 + 4) [After taking LCM and cancelling it]

⇒ 8/10 = 4/5

∴ = 4/5

11. If 3 cot θ = 2, find the value of

Solution:

Given, 3 cot θ = 2

⇒ cot θ = 2/3

From, let’s divide the numerator and denominator by sin θ.

We get,

(4 –3 cot θ) / (2 + 6 cot θ)

⇒ (4 – 3(2/3)) / (2 + 6(2/3)) [using the value of tan θ]

⇒ (4 – 2) / (2 + 4) [After taking LCM and simplifying it]

⇒ 2/6 = 1/3

∴ = 1/3

12. If tan θ = a/b, prove that

Solution:

Given, tan θ = a/b

From LHS, let’s divide the numerator and denominator by cos θ.

And we get,

(a tan θ – b) / (a tan θ + b)

⇒ (a(a/b) – b) / (a(a/b) + b) [using the value of tan θ]

⇒ (a² – b²)/b² / (a² + b²)/b² [After taking LCM and simplifying it]

⇒ (a² – b²)/ (a² + b²)

= RHS

– Hence Proved

13. If sec θ = 13/5, show that

Solution:

Given,

sec θ = 13/5

We know that,

sec θ = 1/ cos θ

⇒ cos θ = 1/ sec θ = 1/ (13/5)

∴ cos θ = 5/13 ……. (1)

By definition,

cos θ = adjacent side/ hypotenuse ….. (2)

Comparing (1) and (2), we have

Adjacent side = 5 and hypotenuse = 13

By Pythagoras’ theorem,

Opposite side = √((hypotenuse) ² – (adjacent side)²)

= √(13² – 5²)

= √(169 – 25)

= √(144)

= 12

Thus, the opposite side = 12

By definition,

tan θ = opposite side/ adjacent side

∴ tan θ = 12/ 5

From, let’s divide the numerator and denominator by cos θ.

We get,

(2 tan θ – 3) / (4 tan θ – 9)

⇒ (2(12/5) – 3) / (4(12/5) – 9) [using the value of tan θ]

⇒ (24 – 15) / (48 – 45) [After taking LCM and cancelling it]

⇒ 9/3 = 3

∴ = 3

14. If cos θ = 12/13, show that sin θ(1 – tan θ) = 35/156

Solution:

Given, cos θ = 12/13…… (1)

By definition, we know that

cos θ = Base side adjacent to ∠θ / Hypotenuse……. (2)

When comparing equations (1) and (2), we get

Base side adjacent to ∠θ = 12 and Hypotenuse = 13

From the figure,

Base side BC = 12

Hypotenuse AC = 13

Side AB is unknown here, and it can be found by using Pythagoras’ theorem.

Thus, by applying Pythagoras’ theorem,

AC² = AB² + BC²

13² = AB² + 12²

Therefore,

AB² = 13² – 12²

AB² = 169 – 144

AB² = 25

AB = √25

AB = 5 …. (3)

Now, we know that

sin θ = Perpendicular side opposite to ∠θ / Hypotenuse

Thus, sin θ = AB/AC [from figure]

⇒ sin θ = 5/13… (4)

And, tan θ = sin θ / cos θ = (5/13) / (12/13)

⇒ tan θ = 12/13… (5)

Taking L.H.S we have

L.H.S = sin θ (1 – tan θ)

Substituting the value of sin θ and tan θ from equations (4) and (5),

We get

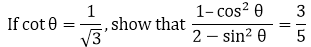
15.

Solution:

Given, cot θ = 1/√3……. (1)

By definition, we know that

cot θ = 1/ tan θ

And, since tan θ = perpendicular side opposite to ∠θ / Base side adjacent to ∠θ

⇒ cot θ = Base side adjacent to ∠θ / perpendicular side opposite to ∠θ …… (2)

On comparing equations (1) and (2), we get

The base side adjacent to ∠θ = 1 and the perpendicular side opposite to ∠θ = √3

Therefore, the triangle formed is,

On substituting the values of known sides as AB = √3 and BC = 1,

AC² = (√3) + 1

AC² = 3 + 1

AC² = 4

AC = √4

Therefore, AC = 2 …   (3)

Now, by definition

sin θ = Perpendicular side opposite to ∠θ / Hypotenuse = AB / AC

⇒ sin θ = √3/ 2 ……(4)

And, cos θ = Base side adjacent to ∠θ / Hypotenuse = BC / AC

⇒ cos θ = 1/ 2 ….. (5)

Now, taking L.H.S., we have

Substituting the values from equations (4) and (5), we have

16.

Solution:

Given, tan θ = 1/ √7 …..(1)

By definition, we know that

tan θ = Perpendicular side opposite to ∠θ / Base side adjacent to ∠θ ……(2)

On comparing equations (1) and (2), we have

The perpendicular side opposite to ∠θ = 1

The base side adjacent to ∠θ = √7

Thus, the triangle representing ∠ θ is,

Hypotenuse AC is unknown, and it can be found by using Pythagoras’ theorem.

By applying Pythagoras’ theorem, we have

AC² = AB² + BC²

AC² = 1² + (√7)²

AC ² = 1 + 7

AC² = 8

AC = √8

⇒ AC = 2√2

By definition,

sin θ = Perpendicular side opposite to ∠θ / Hypotenuse = AB / AC

⇒ sin θ = 1/ 2√2

And, since cosec θ = 1/sin θ

⇒ cosec θ = 2√2 …….. (3)

Now,

cos θ = Base side adjacent to ∠θ / Hypotenuse = BC / AC

⇒ cos θ = √7/ 2√2

And, since sec θ = 1/ sin θ

⇒ sec θ = 2√2/ √7 ……. (4)

Taking the L.H.S of the equation,

Substituting the value of cosec θ and sec θ from equations (3) and (4), we get

17. If sec θ = 5/4, find the value of

Solution:

Given,

sec θ = 5/4

We know that,

sec θ = 1/ cos θ

⇒ cos θ = 1/ (5/4) = 4/5 …… (1)

By definition,

cos θ = Base side adjacent to ∠θ / Hypotenuse …. (2)

On comparing equations (1) and (2), we have

Hypotenuse = 5

The base side adjacent to ∠θ = 4

Thus, the triangle representing ∠ θ is ABC.

The perpendicular side opposite to ∠θ, AB, is unknown, and it can be found by using Pythagoras’ theorem.

By applying Pythagoras’ theorem, we have

AC² = AB² + BC²

AB² = AC² + BC²

AB² = 5² – 4²

AB² = 25 – 16

AB = √9

⇒ AB = 3

By definition,

sin θ = Perpendicular side opposite to ∠θ / Hypotenuse = AB / AC

⇒ sin θ = 3/ 5 …..(3)

Now, tan θ = Perpendicular side opposite to ∠θ / Base side adjacent to ∠θ

⇒ tan θ = 3/ 4 ……(4)

And, since cot θ = 1/ tan θ

⇒ cot θ = 4/ 3 ……(5)

Now,

Substituting the value of sin θ, cos θ, cot θ and tan θ from the equations (1), (3), (4) and (5), we have,

= 12/7

Therefore,

18. If tan θ = 12/13, find the value of

Solution:

Given,

tan θ = 12/13 …….. (1)

We know that, by definition,

tan θ = Perpendicular side opposite to ∠θ / Base side adjacent to ∠θ …… (2)

On comparing equations (1) and (2), we have

The perpendicular side opposite to ∠θ = 12

The base side adjacent to ∠θ = 13

Thus, in the triangle representing ∠ θ, we have,

Hypotenuse AC is unknown, and it can be found by using Pythagoras’ theorem.

So, by applying Pythagoras’ theorem, we have

AC² = 12² + 13²

AC ² = 144 + 169

AC² = 313

⇒ AC = √313

By definition,

sin θ = Perpendicular side opposite to ∠θ / Hypotenuse = AB / AC

⇒ sin θ = 12/ √313…..(3)

And, cos θ = Base side adjacent to ∠θ / Hypotenuse = BC / AC

⇒ cos θ = 13/ √313 …..(4)

Now, substituting the value of sin θ and cos θ from equations (3) and (4), respectively, in the equation below,

Therefore,