RD Sharma Solutions for Class 10 Maths Chapter 11 Constructions

RD Sharma Solutions Class 10 Maths Chapter 11 – Free PDF Download

RD Sharma Solutions for Class 10 Maths Chapter 11 – Constructions is provided here. Scoring good marks in an examination takes a lot of consistent practice and effort. That’s why our expert team at BYJU’S has come up with the RD Sharma Solutions for helping students know the correct procedure of attempting and answering the question of Mathematics. This is definitely a must for all students for an in-depth understanding, last-minute preparations and quick revision of formulae and methods.

Chapter – 11 Constructions of RD Sharma Solutions has three exercises, and you can check the RD Sharma Solutions for Class 10 to educate yourself with the right steps and presentation of these problems. Constructions basically is a continuation from the previous classes, and using that knowledge, various other concepts of geometry like:

• Division of a line segment
• Construction of a triangle similar to a given triangle
• Construction of tangents to a circle

are explained, along with their justifications.

RD Sharma for Class 10 Maths Chapter 11 Constructions here

Download PDF

carouselExampleControls111

Previous



Next

Access Answers to Maths RD Sharma Solutions For Class 10 Chapter 11 – Constructions

Exercise 11.1 Page No: 11.4

1. Determine a point which divides a line segment of length 12 cm internally in the ratio of 2: 3. Also, justify your construction. 

Solution:

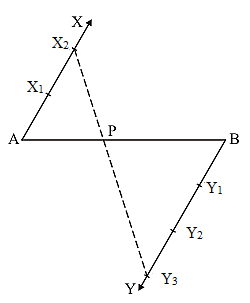
Steps of construction:

1. Draw a line segment AB = 12 cm by using a ruler.

2. Through the points A and B draw two parallel line on the opposite side of AB and making the same acute angles with the line segment.

3. Cut 2 equal parts on AX and 3 equal parts on BY such that AX₁ = X₁X₂ and BY₁ = Y₁Y₂ = Y₂Y₃.

4. Join X₂Y₃ which intersects AB at P

Hence,  AP/PB = 2/3.

Justification:

In ΔAX₂P and ΔBY₃P, we have

∠APX₂ = ∠BPY₃  [vertically opposite angle]

∠X₂AP = ∠Y₃BP  [alternate interior angles}

ΔAX₂P = ΔBY₃P  [Because AA similarity]

∴  AP/BP = AX₂/BY₃ = 2/3  [From C.P.C.T]

Exercise 11.2 Page No: 11.9

1. Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are (2/3) of the corresponding sides of it.
Solution:

Steps of construction:

1. Draw a line segment BC = 5 cm.

2. With centre as B and radius 4 cm and with centre C and radius 6 cm, draw arcs from both points to intersect each other at A.

3. Now, join AB and AC. Then ABC is the triangle.

4. Draw a ray BX making an acute angle with BC and cut off 3 equal parts making BB₁ = B₁B₂= B₂B₃.

5. Join B₃C.

6. Draw B₂ C’ parallel to B₃C and C’A’ parallel to CA.

Then, ΔA’BC’ is the required triangle.

2. Construct a triangle similar to a given ΔABC such that each of its sides is (5/7)^th of the corresponding sides of ΔABC. It is given that AB = 5 cm, BC = 7 cm and ∠ABC = 50°.
Solution:

Steps of construction:

1. Draw a line segment BC = 7 cm.

2. Draw a ray BX making an angle of 50° and cut off BA = 5 cm.

3. Join AC. Then ABC is the triangle.

4. Draw a ray BY making an acute angle with BC and cut off 7 equal parts making BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B_s = B₅B₆ = B₆B₇

5. Now, join B₇ and C

6. Draw B₅C’ parallel to B₇C and C’A’ parallel to CA.

Then, ΔA’BC’ is the required triangle.

3. Construct a triangle similar to a given ΔABC such that each of its sides is (2/3)^rd of the corresponding sides of ΔABC. It is given that BC = 6 cm, ∠B = 50° and ∠C = 60°.
Solution:

Steps of construction:

1. Draw a line segment BC = 6 cm.

2. Draw a ray BX making an angle of 50° and CY making 60° with BC which intersect each other at A. Then, ABC is the triangle.

3. From B, draw another ray BZ making an acute angle below BC and then cut off 3 equal parts making BB₁ = B₁B₂ = B₂B₃

4. Now, join B₃C.

5. From B₂, draw B₂C’ parallel to B₃C and C’A’ parallel to CA.

Then ΔA’BC’ is the required triangle.

4. Draw a ΔABC in which BC = 6 cm, AB = 4 cm and AC = 5 cm. Draw a triangle similar to ΔABC with its sides equal to (3/4)^th of the corresponding sides of ΔABC.
Solution:

Steps of construction:

1. Draw a line segment BC = 6 cm.

2. With centre as B and radius 4 cm and with C as centre and radius 5 cm, draw arcs intersecting each other at A.

3. Join AB and AC. Then, ABC is the triangle.

4. Draw a ray BX making an acute angle with BC and cut off 4 equal parts making BB₁ = B₁B₂ = B₂B₃ = B₃B₄.

5. Join B₄ and C.

6. From B₃ draw C’ parallel to B₄C and from C’, draw C’A’ parallel to CA.

Then ΔA’BC’ is the required triangle.

5. Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are (7/5)^th of the corresponding sides of the first triangle.
Solution:

Steps of construction:

1. Draw a line segment BC = 5 cm.

2. With B as centre and radius 6 cm and with C as centre and radius 7 cm, draw arcs intersecting each other at A.

3. Now, join AB and AC. Then, ABC is the triangle.

4. Draw a ray BX making an acute angle with BC and cut off 7 equal parts making BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇.

5. Join B₅ and C.

6. From B₇, draw B₇C’ parallel to B₅C and C’A’ parallel CA.

Then, ΔA’BC’ is the required triangle.

6. Draw a right triangle ABC in which AC = AB = 4.5 cm and ∠A = 90°. Draw a triangle similar to ΔABC with its sides equal to (5/4)^th of the corresponding sides of ΔABC.
Solution:

Steps of construction:

1. Draw a line segment AB = 4.5 cm.

2. At A, draw a ray AX perpendicular to AB and cut off AC = AB = 4.5 cm.

3. Now, join BC. Then, ABC is the triangle.

4. Draw a ray AY making an acute angle with AB and cut off 5 equal parts making AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅

5. Join A₄ and B.

6. From A₅, draw A₅B’ parallel to  A₄B and  B’C’ parallel to BC.

Then, ΔAB’C’ is the required triangle.

7. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 5 cm and 4 cm. Then construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle.
Solution:

Steps of construction:

1. Draw a line segment BC = 5 cm.

2. At B, draw perpendicular BX and cut off BA = 4 cm.

3. Now, join AC. Then, ABC is the triangle

4. Draw a ray BY making an acute angle with BC and cut off 5 equal parts making BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅

5. Join B₃ and C.

6. From B₅, draw B₅C’ parallel to B₃C and C’A’ parallel to CA.

Then, ΔA’BC’ is the required triangle.

Exercise 11.3 Page No: 11.17

1. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct a pair of tangents to the circle and measure their lengths.

Solution:

Steps of construction:

1. Firstly, we draw a circle with centre O and radius 6 cm.

2. Mark a point P at a distance of OP = 10 cm, and join OP.

3. Draw a right bisector of OP, intersecting OP at Q.

4. Now, taking Q as centre and radius OQ = PQ, draw a circle to intersect the given circle at T and T’.

5. Join PT and PT’ to obtain the required tangents.

Thus, PT and PT’ are the required tangents.

To find the length of the tangents.

We know that OT ⊥ PT and ΔOTP is the right triangle.

Therefore, OT = 6 cm (radius) and PO = 10 cm.

So, in ΔOTP,

PT²  = OP² − OT² [By Pythagoras theorem]

= (10)² − (6)²

= 100 – 36

= 64

= 8 cm

Therefore, the length of tangents is 8 cm each.

​2. Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these points P and Q.

Solution:

Steps of construction:

1. Draw a line segment PQ of 14 cm.

2. Now, mark the midpoint O of PQ.

3. Draw the perpendicular bisectors of PO and OQ which intersects at points R and S on PQ.

4. With centre R and radius RP draw a circle.

5. With centre S and radius, SQ draw a circle.

6. And now, with centre O and radius 3 cm draw another circle which intersects the previous circles at the points A, B, C, and D.

7. Finally, join PA, PB, QC and QD.

Thus, PA, PB, QC, and QD are the required tangents.

​3. Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as the centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.

Solution:

Steps of construction:

1. Draw a line segment AB = 8 cm.

2. Draw the perpendicular of AB which intersects it at C.

3. With the centre, C and radius CA draw a circle.

4. Now, with A & B as centres and radii 4 cm and 3 cm respectively, draw two circles which intersects the previous circles at the points P, Q, R and S.

5. Finally, join AR, AS, BP and BQ.

Thus, AR, AS, BP and BQ are the required tangents.