RD Sharma Solutions Class 10 Maths Chapter 7 – Free PDF Download
RD Sharma Solutions for Class 10 Maths Chapter 7 – Statistics are provided here for students to access easily. If students are looking for a last-minute reference source, then RD Sharma Solutions is like the best friend who brushes up on all the important concepts and their formulas. Furthermore, this is an essential tool to qualify for the exams with high marks. It is created by our team of experts at BYJU’S, keeping in mind the latest CBSE norms and also in simple language with suitable explanations.
One of the interesting chapters of RD Sharma Class 10 Statistics, it is the 7th chapter and comprises six exercises. Students can access the answers to the exercises included in RD Sharma Solutions for Class 10 here. The chapter basically deals with the techniques for finding the mean, median and mode of grouped data. It also includes the concept of a cumulative frequency graph of a frequency distribution.
RD Sharma Solutions for Class 10 Maths Chapter 7 Statistics Here
RD Sharma Solutions for Class 10 Maths Chapter 7 Statistics – Exercise-wise
Access the RD Sharma Solutions for Class 10 Maths Chapter 7 – Statistics
RD Sharma Solutions for Class 10 Maths Chapter 7 Exercise 7.1 Page No: 7.5
1. Calculate the mean for the following distribution.
| x: | 5 | 6 | 7 | 8 | 9 |
| f: | 4 | 8 | 14 | 11 | 3 |
Solution:
| x | f | fx |
| 5 | 4 | 20 |
| 6 | 8 | 48 |
| 7 | 14 | 98 |
| 8 | 11 | 88 |
| 9 | 3 | 27 |
| N = 40 | Σ fx = 281 |
Mean = Σ fx/ N = 281/40
∴ Mean = 7.025
2. Find the mean of the following data.
| x: | 19 | 21 | 23 | 25 | 27 | 29 | 31 |
| f: | 13 | 15 | 16 | 18 | 16 | 15 | 13 |
Solution:
| x | f | fx |
| 19 | 13 | 247 |
| 21 | 15 | 315 |
| 23 | 16 | 368 |
| 25 | 18 | 450 |
| 27 | 16 | 432 |
| 29 | 15 | 435 |
| 31 | 13 | 403 |
| N = 106 | Σ fx = 2620 |
Mean = Σ fx/ N = 2620/106
∴ Mean = 25
3. If the mean of the following data is 20.6. Find the value of p.
| x: | 10 | 15 | p | 25 | 35 |
| f: | 3 | 10 | 25 | 7 | 5 |
Solution:
| x | f | fx |
| 10 | 3 | 30 |
| 15 | 10 | 150 |
| p | 25 | 25p |
| 25 | 7 | 175 |
| 35 | 5 | 175 |
| N = 50 | Σ fx = 530 + 25p |
We know that,
Mean = Σ fx/ N = (2620 + 25p)/ 50
Given,
Mean = 20.6
⇒ 20.6 = (530 + 25p)/ 50
(20.6 x 50) – 530 = 25p
p = 500/ 25
∴ p = 20
4. If the mean of the following data is 15, find p.
| x: | 5 | 10 | 15 | 20 | 25 |
| f: | 6 | p | 6 | 10 | 5 |
Solution:
| x | f | fx |
| 5 | 6 | 30 |
| 10 | p | 10p |
| 15 | 6 | 90 |
| 20 | 10 | 200 |
| 25 | 5 | 125 |
| N = p + 27 | Σ fx = 445 + 10p |
We know that,
Mean = Σ fx/ N = (445 + 10p)/ (p + 27)
Given,
Mean = 15
⇒ 15 = (445 + 10p)/ (p + 27)
15p + 405 = 445 + 10p
5p = 40
∴ p = 8
5. Find the value of p for the following distribution, whose mean is 16.6.
| x: | 8 | 12 | 15 | p | 20 | 25 | 30 |
| f: | 12 | 16 | 20 | 24 | 16 | 8 | 4 |
Solution:
| x | f | fx |
| 8 | 12 | 96 |
| 12 | 16 | 192 |
| 15 | 20 | 300 |
| P | 24 | 24p |
| 20 | 16 | 320 |
| 25 | 8 | 200 |
| 30 | 4 | 120 |
| N = 100 | Σ fx = 1228 + 24p |
We know that,
Mean = Σ fx/ N = (1228 + 24p)/ 100
Given,
Mean = 16.6
⇒ 16.6 = (1228 + 24p)/ 100
1660 = 1228 + 24p
24p = 432
∴ p = 18
6. Find the missing value of p for the following distribution, whose mean is 12.58.
| x: | 5 | 8 | 10 | 12 | p | 20 | 25 |
| f: | 2 | 5 | 8 | 22 | 7 | 4 | 2 |
Solution:
| x | f | fx |
| 5 | 2 | 10 |
| 8 | 5 | 40 |
| 10 | 8 | 80 |
| 12 | 22 | 264 |
| P | 7 | 7p |
| 20 | 4 | 80 |
| 25 | 2 | 50 |
| N = 50 | Σ fx = 524 + 7p |
We know that,
Mean = Σ fx/ N = (524 + 7p)/ 50
Given,
Mean = 12.58
⇒ 12.58 = (524 + 7p)/ 50
629 = 524 + 7p
7p = 629 – 524 = 105
∴ p = 15
7. Find the missing frequency (p) for the following distribution, whose mean is 7.68.
| x: | 3 | 5 | 7 | 9 | 11 | 13 |
| f: | 6 | 8 | 15 | p | 8 | 4 |
Solution:
| x | f | fx |
| 3 | 6 | 18 |
| 5 | 8 | 40 |
| 7 | 15 | 105 |
| 9 | p | 9p |
| 11 | 8 | 88 |
| 13 | 4 | 52 |
| N = 41 + p | Σ fx = 303 + 9p |
We know that,
Mean = Σ fx/ N = (303 + 9p)/ (41 + p)
Given,
Mean = 7.68
⇒ 7.68 = (303 + 9p)/ (41 + p)
7.68(41 + p) = 303 + 9p
7.68p + 314.88 = 303 + 9p
1.32p = 11.88
∴ p = 11.88/1.32 = 9
RD Sharma Solutions for Class 10 Maths Chapter 7 Exercise 7.2 Page No: 7.5
1. The number of telephone calls received at an exchange per interval for 250 successive one-minute intervals is given in the following frequency table.
| No. of calls (x) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| No. of intervals (f) | 15 | 24 | 29 | 46 | 54 | 43 | 39 |
Compute the mean number of calls per interval.
Solution:
Let the assumed mean(A) = 3
| No. of calls xi | No. of intervals fi | ui = xi – A = xi – 3 | fi ui |
| 0 | 15 | -3 | -45 |
| 1 | 24 | -2 | -48 |
| 2 | 29 | -1 | -29 |
| 3 | 46 | 0 | 0 |
| 4 | 54 | 1 | 54 |
| 5 | 43 | 2 | 86 |
| 6 | 39 | 3 | 117 |
| N = 250 | Σ fixi = 135 |
Mean number of calls = A + Σ fixi / N
= 3 + 135/250
= (750 + 135)/ 250 = 885/ 250
= 3.54
2. Five coins were simultaneously tossed 1000 times, and at each toss, the number of heads was observed. The number of tosses during which 0, 1, 2, 3, 4 and 5 heads were obtained are shown in the table below. Find the mean number of heads per toss.
| No. of heads per toss (x) | 0 | 1 | 2 | 3 | 4 | 5 |
| No. of tosses (f) | 38 | 144 | 342 | 287 | 164 | 25 |
Solution:
Let the assumed mean(A) = 2
| No. of heads per toss xi | No. of intervals fi | ui = xi – A = xi – 2 | fi ui |
| 0 | 38 | -2 | -76 |
| 1 | 144 | -1 | -144 |
| 2 | 342 | 0 | 0 |
| 3 | 287 | 1 | 287 |
| 4 | 164 | 2 | 328 |
| 5 | 25 | 3 | 75 |
| N = 1000 | Σ fixi = 470 |
Mean number of heads per toss = A + Σ fixi / N
= 2 + 470/1000
= 2 + 0.470
= 2.470
3. The following table gives the number of branches and number of plants in the garden of a school.
| No of branches (x) | 2 | 3 | 4 | 5 | 6 |
| No of plants (f) | 49 | 43 | 57 | 38 | 13 |
Calculate the average number of branches per plant.
Solution:
Let the assumed mean (A) = 4
| No. of branches xi | No. of plants fi | ui = xi − A = xi − 4 | fi ui |
| 2 | 49 | -2 | -98 |
| 3 | 43 | -1 | -43 |
| 4 | 57 | 0 | 0 |
| 5 | 38 | 1 | 38 |
| 6 | 13 | 2 | 26 |
| N = 200 | Σ fixi = -77 |
Average number of branches per plant = A + Σ fixi / N = 4 + (-77/200)
= 4 -77/200
= (800 -77)/200
= 3.615
4. The following table gives the number of children of 150 families in a village.
| No of children (x) | 0 | 1 | 2 | 3 | 4 | 5 |
| No of families (f) | 10 | 21 | 55 | 42 | 15 | 7 |
Find the average number of children per family.
Solution:
Let the assumed mean (A) = 2
| No. of children xi | No. of families fi | ui = xi − A = xi − 2 | fi ui |
| 0 | 10 | -2 | -20 |
| 1 | 21 | -1 | -21 |
| 2 | 55 | 0 | 0 |
| 3 | 42 | 1 | 42 |
| 4 | 15 | 2 | 30 |
| 5 | 7 | 3 | 21 |
| N = 150 | Σ fixi = 52 |
Average number of children for family = A + Σ fixi / N = 2 + 52/150
= (300 +52)/150
= 352/150
= 2.35 (corrected to neat decimal)
RD Sharma Solutions for Class 10 Maths Chapter 7 Exercise 7.3 Page No: 7.22
1. The following table gives the distribution of total household expenditure (in rupees) of manual workers in a city.
| Expenditure (in rupees) (x) | Frequency (fi) | Expenditure (in rupees) (xi) | Frequency (fi) |
| 100 – 150 | 24 | 300 – 350 | 30 |
| 150 – 200 | 40 | 350 – 400 | 22 |
| 200 – 250 | 33 | 400 – 450 | 16 |
| 250 – 300 | 28 | 450 – 500 | 7 |
Find the average expenditure (in rupees) per household.
Solution:
Let the assumed mean (A) = 275
| Class interval | Mid value (xi) | di = xi – 275 | ui = (xi – 275)/50 | Frequency fi | fiui |
| 100 – 150 | 125 | -150 | -3 | 24 | -72 |
| 150 – 200 | 175 | -100 | -2 | 40 | -80 |
| 200 – 250 | 225 | -50 | -1 | 33 | -33 |
| 250 – 300 | 275 | 0 | 0 | 28 | 0 |
| 300 – 350 | 325 | 50 | 1 | 30 | 30 |
| 350 – 400 | 375 | 100 | 2 | 22 | 44 |
| 400 – 450 | 425 | 150 | 3 | 16 | 48 |
| 450 – 500 | 475 | 200 | 4 | 7 | 28 |
| N = 200 | Σ fiui = -35 |
It’s seen that A = 275 and h = 50
So,
Mean = A + h x (Σfi ui/N)
= 275 + 50 (-35/200)
= 275 – 8.75
= 266.25
2. A survey was conducted by a group of students as a part of their environmental awareness program, in which they collected the following data regarding the number of plants in 200 houses in a locality. Find the mean number of plants per house.
| Number of plants | 0 – 2 | 2 – 4 | 4 – 6 | 6 – 8 | 8 – 10 | 10 – 12 | 12 – 14 |
| Number of houses | 1 | 2 | 1 | 5 | 6 | 2 | 3 |
Which method did you use for finding the mean, and why?
Solution:
From the given data,
To find the class interval, we know that,
Classmarks (xi) = (upper class limit + lower class limit)/2
Now, let’s compute xi and fixi by the following:
| Number of plants | Number of houses (fi) | xi | fixi |
| 0 – 2 | 1 | 1 | 1 |
| 2 – 4 | 2 | 3 | 6 |
| 4 – 6 | 1 | 5 | 5 |
| 6 – 8 | 5 | 7 | 35 |
| 8 – 10 | 6 | 9 | 54 |
| 10 – 12 | 2 | 11 | 22 |
| 12 – 14 | 3 | 13 | 39 |
| Total | N = 20 | Σ fiui = 162 |
Here,
Mean = Σ fiui / N
= 162/ 20
= 8.1
Thus, the mean number of plants in a house is 8.1.
We have used the direct method, as the values of class mark xi and fi are very small.
3. Consider the following distribution of daily wages of workers of a factory.
| Daily wages (in ₹) | 100 – 120 | 120 – 140 | 140 – 160 | 160 – 180 | 180 – 200 |
| Number of workers | 12 | 14 | 8 | 6 | 10 |
Find the mean daily wages of the workers of the factory by using an appropriate method.
Solution:
Let the assumed mean (A) = 150
| Class interval | Mid value xi | di = xi – 150 | ui = (xi – 150)/20 | Frequency fi | fiui |
| 100 – 120 | 110 | -40 | -2 | 12 | -24 |
| 120 – 140 | 130 | -20 | -1 | 14 | -14 |
| 140 – 160 | 150 | 0 | 0 | 8 | 0 |
| 160 – 180 | 170 | 20 | 1 | 6 | 6 |
| 180 – 200 | 190 | 40 | 2 | 10 | 20 |
| N= 50 | Σ fiui = -12 |
It’s seen that,
A = 150 and h = 20
So,
Mean = A + h x (Σfi ui/N)
= 150 + 20 x (-12/50)
= 150 – 24/5
= 150 = 4.8
= 145.20
4. Thirty women were examined in a hospital by a doctor, and the number of heartbeats per minute recorded and summarised is as follows. Find the mean heartbeats per minute for these women, choosing a suitable method.
| Number of heartbeats per minute | 65 – 68 | 68 – 71 | 71 – 74 | 74 – 77 | 77 – 80 | 80 – 83 | 83 – 86 |
| Number of women | 2 | 4 | 3 | 8 | 7 | 4 | 2 |
Solution:
Using the relation (xi) = (Upper class limit + Lower class limit)/ 2
And class size of this data = 3
Let the assumed mean (A) = 75.5
So, let’s calculate di, ui, fiui as follows:
| Number of heartbeats per minute | Number of women (fi) | xi | di = xi – 75.5 | ui = (xi – 755)/h | fiui |
| 65 – 68 | 2 | 66.5 | -9 | -3 | -6 |
| 68 – 71 | 4 | 69.5 | -6 | -2 | -8 |
| 71 – 74 | 3 | 72.5 | -3 | -1 | -3 |
| 74 – 77 | 8 | 75.5 | 0 | 0 | 0 |
| 77 – 80 | 7 | 78.5 | 3 | 1 | 7 |
| 80 – 83 | 4 | 81.5 | 6 | 2 | 8 |
| 83 – 86 | 2 | 84.5 | 9 | 3 | 6 |
| N = 30 | Σ fiui = 4 |
From the table, it’s seen that
N = 30 and h = 3
So, the mean = A + h x (Σfi ui/N)
= 75.5 + 3 x (4/30
= 75.5 + 2/5
= 75.9
Therefore, the mean heartbeats per minute for those women are 75.9 beats per minute.
Find the mean of each of the following frequency distributions: (5 – 14)
5.
| Class interval: | 0 – 6 | 6 – 12 | 12 – 18 | 18 – 24 | 24 – 30 |
| Frequency: | 6 | 8 | 10 | 9 | 7 |
Solution:
Let’s consider the assumed mean (A) = 15
| Class interval | Mid-value xi | di = xi – 15 | ui = (xi – 15)/6 | fi | fiui |
| 0 – 6 | 3 | -12 | -2 | 6 | -12 |
| 6 – 12 | 9 | -6 | -1 | 8 | -8 |
| 12 – 18 | 15 | 0 | 0 | 10 | 0 |
| 18 – 24 | 21 | 6 | 1 | 9 | 9 |
| 24 – 30 | 27 | 12 | 2 | 7 | 14 |
| N = 40 | Σ fiui = 3 |
From the table, it’s seen that
A = 15 and h = 6
Mean = A + h x (Σfi ui/N)
= 15 + 6 x (3/40)
= 15 + 0.45
= 15.45
6.
| Class interval: | 50 – 70 | 70 – 90 | 90 – 110 | 110 – 130 | 130 – 150 | 150 – 170 |
| Frequency: | 18 | 12 | 13 | 27 | 8 | 22 |
Solution:
Let’s consider the assumed mean (A) = 100
| Class interval | Mid-value xi | di = xi – 100 | ui = (xi – 100)/20 | fi | fiui |
| 50 – 70 | 60 | -40 | -2 | 18 | -36 |
| 70 – 90 | 80 | -20 | -1 | 12 | -12 |
| 90 – 110 | 100 | 0 | 0 | 13 | 0 |
| 110 – 130 | 120 | 20 | 1 | 27 | 27 |
| 130 – 150 | 140 | 40 | 2 | 8 | 16 |
| 150 – 170 | 160 | 60 | 3 | 22 | 66 |
| N= 100 | Σ fiui = 61 |
From the table, it’s seen that
A = 100 and h = 20
Mean = A + h x (Σfi ui/N)
= 100 + 20 x (61/100)
= 100 + 12.2
= 112.2
7.
| Class interval | 0 – 8 | 8 – 16 | 16 – 24 | 24 – 32 | 32 – 40 |
| Frequency | 6 | 7 | 10 | 8 | 9 |
Solution:
Let’s consider the assumed mean (A) = 20
| Class interval | Mid-value xi | di = xi – 20 | ui = (xi – 20)/8 | fi | fiui |
| 0 – 8 | 4 | -16 | -2 | 6 | -12 |
| 8 – 16 | 12 | -8 | -1 | 7 | -7 |
| 16 – 24 | 20 | 0 | 0 | 10 | 0 |
| 24 – 32 | 28 | 8 | 1 | 8 | 8 |
| 32 – 40 | 36 | 16 | 2 | 9 | 18 |
| N = 40 | Σ fiui = 7 |
From the table, it’s seen that
A = 20 and h = 8
Mean = A + h x (Σfi ui/N)
= 20 + 8 x (7/40)
= 20 + 1.4
= 21.4
8.
| Class intervaL | 0 – 6 | 6 – 12 | 12 – 18 | 18 – 24 | 24 – 30 |
| Frequency | 7 | 5 | 10 | 12 | 6 |
Solution:
Let’s consider the assumed mean (A) = 15
| Class interval | Mid-value xi | di = xi – 15 | ui = (xi – 15)/6 | fi | fiui |
| 0 – 6 | 3 | -12 | -2 | 7 | -14 |
| 6 – 12 | 9 | -6 | -1 | 5 | -5 |
| 12 – 18 | 15 | 0 | 0 | 10 | 0 |
| 18 – 24 | 21 | 6 | 1 | 12 | 12 |
| 24 – 30 | 27 | 12 | 2 | 6 | 12 |
| N = 40 | Σ fiui = 5 |
From the table, it’s seen that
A = 15 and h = 6
Mean = A + h x (Σfi ui/N)
= 15 + 6 x (5/40)
= 15 + 0.75
= 15.75
9.
| Class interval | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| Frequency | 9 | 12 | 15 | 10 | 14 |
Solution:
Let’s consider the assumed mean (A) = 25
| Class interval | Mid-value xi | di = xi – 25 | ui = (xi – 25)/10 | fi | fiui |
| 0 – 10 | 5 | -20 | -2 | 9 | -18 |
| 10 – 20 | 15 | -10 | -1 | 12 | -12 |
| 20 – 30 | 25 | 0 | 0 | 15 | 0 |
| 30 – 40 | 35 | 10 | 1 | 10 | 10 |
| 40 – 50 | 45 | 20 | 2 | 14 | 28 |
| N = 60 | Σ fiui = 8 |
From the table, it’s seen that
A = 25 and h = 10
Mean = A + h x (Σfi ui/N)
= 25 + 10 x (8/60)
= 25 + 4/3
= 79/3 = 26.333
10.
| Class interval | 0 – 8 | 8 – 16 | 16 – 24 | 24 – 32 | 32 – 40 |
| Frequency | 5 | 9 | 10 | 8 | 8 |
Solution:
Let’s consider the assumed mean (A) = 20
| Class interval | Mid-value xi | di = xi – 20 | ui = (xi – 20)/8 | fi | fiui |
| 0 – 8 | 4 | -16 | -2 | 5 | -10 |
| 8 – 16 | 12 | -4 | -1 | 9 | -9 |
| 16 – 24 | 20 | 0 | 0 | 10 | 0 |
| 24 – 32 | 28 | 4 | 1 | 8 | 8 |
| 32 – 40 | 36 | 16 | 2 | 8 | 16 |
| N = 40 | Σ fiui = 5 |
From the table, it’s seen that
A = 20 and h = 8
Mean = A + h x (Σfi ui/N)
= 20 + 8 x (5/40)
= 20 + 1
= 21
11.
| Class interval | 0 – 8 | 8 – 16 | 16 – 24 | 24 – 32 | 32 – 40 |
| Frequency | 5 | 6 | 4 | 3 | 2 |
Solution:
Let’s consider the assumed mean (A) = 20
| Class interval | Mid-value xi | di = xi – 20 | ui = (xi – 20)/8 | fi | fiui |
| 0 – 8 | 4 | -16 | -2 | 5 | -12 |
| 8 – 16 | 12 | -8 | -1 | 6 | -8 |
| 16 – 24 | 20 | 0 | 0 | 4 | 0 |
| 24 – 32 | 28 | 8 | 1 | 3 | 9 |
| 32 – 40 | 36 | 16 | 2 | 2 | 14 |
| N = 20 | Σ fiui = -9 |
From the table, it’s seen that
A = 20 and h = 8
Mean = A + h x (Σfi ui/N)
= 20 + 6 x (-9/20)
= 20 – 72/20
= 20 – 3.6
= 16.4
12.
| Class interval | 10 – 30 | 30 – 50 | 50 – 70 | 70 – 90 | 90 – 110 | 110 – 130 |
| Frequency | 5 | 8 | 12 | 20 | 3 | 2 |
Solution:
Let’s consider the assumed mean (A) = 60
| Class interval | Mid-value xi | di = xi –60 | ui = (xi – 60)/20 | fi | fiui |
| 10 – 30 | 20 | -40 | -2 | 5 | -10 |
| 30 – 50 | 40 | -20 | -1 | 8 | -8 |
| 50 – 70 | 60 | 0 | 0 | 12 | 0 |
| 70 – 90 | 80 | 20 | 1 | 20 | 20 |
| 90 – 110 | 100 | 40 | 2 | 3 | 6 |
| 110 – 130 | 120 | 60 | 3 | 2 | 6 |
| N = 50 | Σ fiui = 14 |
From the table, it’s seen that
A = 60 and h = 20
Mean = A + h x (Σfi ui/N)
= 60 + 20 x (14/50)
= 60 + 28/5
= 60 + 5.6
= 65.6
13.
| Class interval | 25 – 35 | 35 – 45 | 45 – 55 | 55 – 65 | 65 – 75 |
| Frequency | 6 | 10 | 8 | 12 | 4 |
Solution:
Let’s consider the assumed mean (A) = 50
| Class interval | Mid-value xi | di = xi – 50 | ui = (xi – 50)/10 | fi | fiui |
| 25 – 35 | 30 | -20 | -2 | 6 | -12 |
| 35 – 45 | 40 | -10 | -1 | 10 | -10 |
| 45 – 55 | 50 | 0 | 0 | 8 | 0 |
| 55 – 65 | 60 | 10 | 1 | 12 | 12 |
| 65 – 75 | 70 | 20 | 2 | 4 | 8 |
| N = 40 | Σ fiui = -2 |
From the table, it’s seen that
A = 50 and h = 10
Mean = A + h x (Σfi ui/N)
= 50 + 10 x (-2/40)
= 50 – 0.5
= 49.5
14.
| Class interval | 25 – 29 | 30 – 34 | 35 – 39 | 40 – 44 | 45 – 49 | 50 – 54 | 55 – 59 |
| Frequency | 14 | 22 | 16 | 6 | 5 | 3 | 4 |
Solution:
Let’s consider the assumed mean (A) = 42
| Class interval | Mid-value xi | di = xi – 42 | ui = (xi – 42)/5 | fi | fiui |
| 25 – 29 | 27 | -15 | -3 | 14 | -42 |
| 30 – 34 | 32 | -10 | -2 | 22 | -44 |
| 35 – 39 | 37 | -5 | -1 | 16 | -16 |
| 40 – 44 | 42 | 0 | 0 | 6 | 0 |
| 45 – 49 | 47 | 5 | 1 | 5 | 5 |
| 50 – 54 | 52 | 10 | 2 | 3 | 6 |
| 55 – 59 | 57 | 15 | 3 | 4 | 12 |
| N = 70 | Σ fiui = -79 |
From the table, it’s seen that
A = 42 and h = 5
Mean = A + h x (Σfi ui/N)
= 42 + 5 x (-79/70)
= 42 – 79/14
= 42 – 5.643
= 36.357
RD Sharma Solutions for Class 10 Maths Chapter 7 Exercise 7.4 Page No: 7.34
1. Following are the lives in hours of 15 pieces of the components of an aircraft engine. Find the median.
715, 724, 725, 710, 729, 745, 694, 699, 696, 712, 734, 728, 716, 705, 719.
Solution:
Arranging the given data in ascending order, we have
694, 696, 699, 705, 710, 712, 715, 716, 719, 721, 725, 728, 729, 734, 745
As the number of terms is an old number, i.e., N = 15
We use the following procedure to find the median.
Median = (N + 1)/2 th term
= (15 + 1)/2 th term
= 8th term
So, the 8th term in the arranged order of the given data should be the median.
Therefore, 716 is the median of the data.
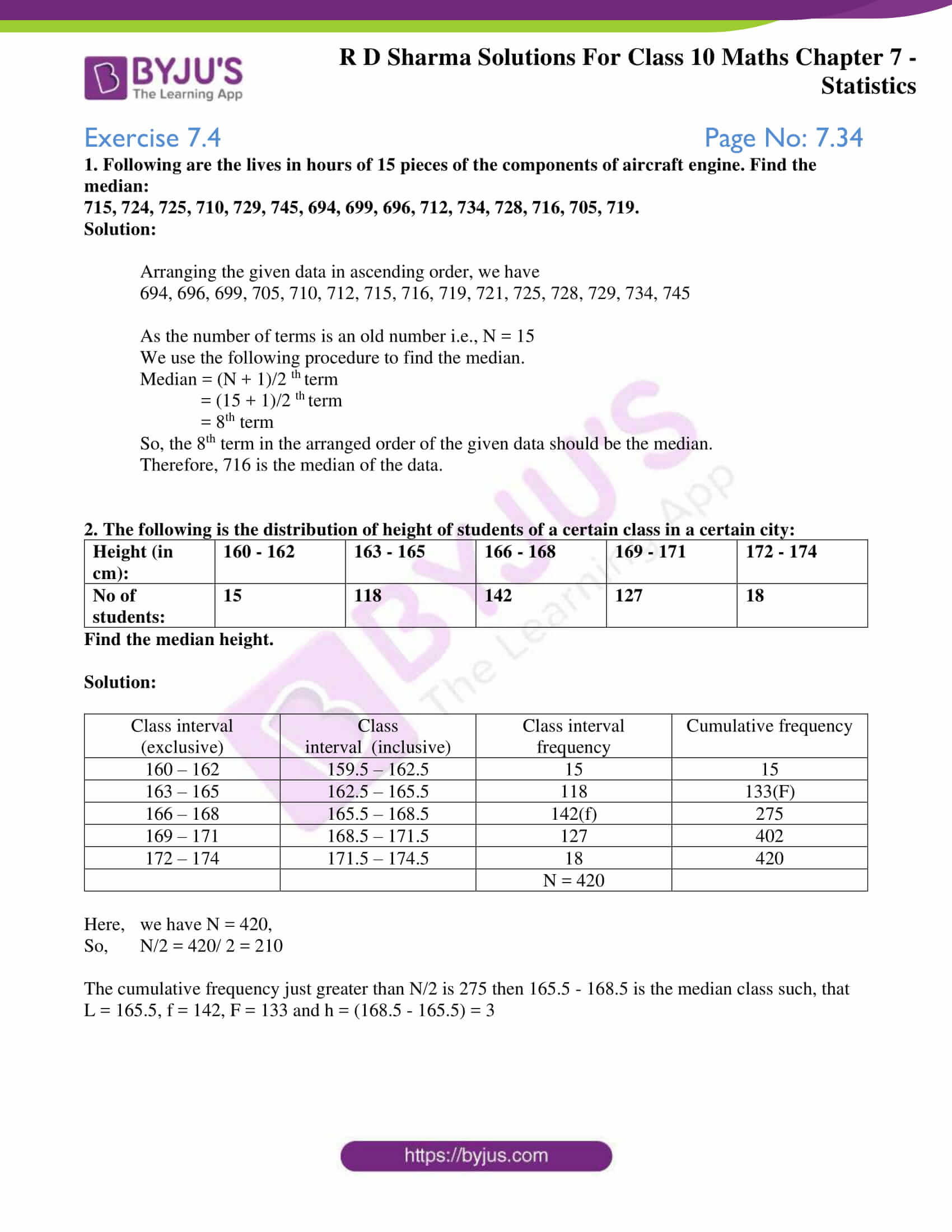
2. The following is the distribution of the height of students of a certain class in a certain city:
| Height (in cm) | 160 – 162 | 163 – 165 | 166 – 168 | 169 – 171 | 172 – 174 |
| No. of students | 15 | 118 | 142 | 127 | 18 |
Find the median height.
Solution:
| Class interval (exclusive) | Class interval (inclusive) | Class interval frequency | Cumulative frequency |
| 160 – 162 | 159.5 – 162.5 | 15 | 15 |
| 163 – 165 | 162.5 – 165.5 | 118 | 133(F) |
| 166 – 168 | 165.5 – 168.5 | 142(f) | 275 |
| 169 – 171 | 168.5 – 171.5 | 127 | 402 |
| 172 – 174 | 171.5 – 174.5 | 18 | 420 |
| N = 420 |
Here, we have N = 420,
So, N/2 = 420/ 2 = 210
The cumulative frequency just greater than N/2 is 275, then 165.5 – 168.5 is the median class, such that
L = 165.5, f = 142, F = 133 and h = (168.5 – 165.5) = 3

= 165.5 + 1.63
= 167.13
3. Following is the distribution of I.Q. of 100 students. Find the median I.Q.
| I.Q: | 55 – 64 | 65 – 74 | 75 – 84 | 85 – 94 | 95 – 104 | 105 – 114 | 115 – 124 | 125 – 134 | 135 – 144 |
| No of students: | 1 | 2 | 9 | 22 | 33 | 22 | 8 | 2 | 1 |
Solution:
| Class interval (exclusive) | Class interval (inclusive) | Class interval frequency | Cumulative frequency |
| 55 – 64 | 54.5 – 64-5 | 1 | 1 |
| 65 – 74 | 64.5 – 74.5 | 2 | 3 |
| 75 – 84 | 74.5 – 84.5 | 9 | 12 |
| 85 – 94 | 84.5 – 94.5 | 22 | 34(F) |
| 95 – 104 | 94.5 – 104.5 | 33(f) | 67 |
| 105 – 114 | 104.5 – 114.5 | 22 | 89 |
| 115 – 124 | 114.5 – 124.5 | 8 | 97 |
| 125 – 134 | 124.5 – 134.5 | 2 | 98 |
| 135 – 144 | 134.5 – 144.5 | 1 | 100 |
| N = 100 |
Here, we have N = 100,
So, N/2 = 100/ 2 = 50
The cumulative frequency just greater than N/ 2 is 67, then the median class is (94.5 – 104.5), such that L = 94.5, F = 33, h = (104.5 – 94.5) = 10

= 94.5 + 4.85
= 99.35
4. Calculate the median from the following data:
| Rent (in Rs): | 15 – 25 | 25 – 35 | 35 – 45 | 45 – 55 | 55 – 65 | 65 – 75 | 75 – 85 | 85 – 95 |
| No of houses: | 8 | 10 | 15 | 25 | 40 | 20 | 15 | 7 |
Solution:
| Class interval | Frequency | Cumulative frequency |
| 15 – 25 | 8 | 8 |
| 25 – 35 | 10 | 18 |
| 35 – 45 | 15 | 33 |
| 45 – 55 | 25 | 58(F) |
| 55 – 65 | 40(f) | 98 |
| 65 – 75 | 20 | 118 |
| 75 – 85 | 15 | 133 |
| 85 – 95 | 7 | 140 |
| N = 140 |
Here, we have N = 140,
So, N/2 = 140/ 2 = 70
The cumulative frequency just greater than N/ 2 is 98, then median class is 55 – 65, such that L = 55, f = 40, F = 58, h = 65 – 55 = 10

= 55 + 3 = 58
5. Calculate the median from the following data:
| Marks below: | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 | 70 – 80 | 85 – 95 |
| No of students: | 15 | 35 | 60 | 84 | 96 | 127 | 198 | 250 |
Solution:
| Marks below | No. of students | Class interval | Frequency | Cumulative frequency |
| 10 | 15 | 0 – 10 | 15 | 15 |
| 20 | 35 | 10 – 20 | 20 | 35 |
| 30 | 60 | 20 – 30 | 25 | 60 |
| 40 | 84 | 30 – 40 | 24 | 84 |
| 50 | 96 | 40 – 50 | 12 | 96(F) |
| 60 | 127 | 50 – 60 | 31(f) | 127 |
| 70 | 198 | 60 – 70 | 71 | 198 |
| 80 | 250 | 70 – 80 | 52 | 250 |
| N = 250 |
Here, we have N = 250,
So, N/2 = 250/ 2 = 125
The cumulative frequency just greater than N/ 2 is 127, then median class is 50 – 60, such that L = 50, f = 31, F = 96, h = 60 -50 = 10

= 50 + 9.35
= 59.35
6. Calculate the missing frequency from the following distribution, it being given that the median of the distribution is 24.
| Age in years: | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| No of persons: | 5 | 25 | ? | 18 | 7 |
Solution:
Let the unknown frequency be taken as x,
| Class interval | Frequency | Cumulative frequency |
| 0 – 10 | 5 | 5 |
| 10 – 20 | 25 | 30(F) |
| 20 – 30 | x (f) | 30 + x |
| 30 – 40 | 18 | 48 + x |
| 40 – 50 | 7 | 55 + x |
| N = 170 |
It’s given that
Median = 24
Then, median class = 20 – 30; L = 20, h = 30 -20 = 10, f = x, F = 30

4x = 275 + 5x – 300
4x – 5x = – 25
– x = – 25
x = 25
Therefore, the Missing frequency = 25
7. The following table gives the frequency distribution of married women by age at marriage.
| Age (in years) | Frequency | Age (in years) | Frequency |
| 15 – 19 | 53 | 40 – 44 | 9 |
| 20 – 24 | 140 | 45 – 49 | 5 |
| 25 – 29 | 98 | 45 – 49 | 3 |
| 30 – 34 | 32 | 55 – 59 | 3 |
| 35 – 39 | 12 | 60 and above | 2 |
Calculate the median and interpret the results.
Solution:
| Class interval (exclusive) | Class interval (inclusive) | Frequency | Cumulative frequency |
| 15 – 19 | 14.5 – 19.5 | 53 | 53 (F) |
| 20 – 24 | 19.5 – 24.5 | 140 (f) | 193 |
| 25 – 29 | 24.5 – 29.5 | 98 | 291 |
| 30 – 34 | 29.5 – 34.5 | 32 | 323 |
| 35 – 39 | 34.5 – 39.5 | 12 | 335 |
| 40 – 44 | 39.5 – 44.5 | 9 | 344 |
| 45 – 49 | 44.5 – 49.5 | 5 | 349 |
| 50 – 54 | 49.5 – 54.5 | 3 | 352 |
| 55 – 54 | 54.5 – 59.5 | 3 | 355 |
| 60 and above | 59.5 and above | 2 | 357 |
| N =357 |
Here, we have N = 357,
So, N/2 = 357/ 2 = 178.5
The cumulative frequency just greater than N/2 is 193, so then the median class is (19.5 – 24.5), such that l = 19.5, f = 140, F = 53, h = 25.5 – 19.5 = 5

Median = 23.98
This means nearly half the women were married between the ages of 15 and 25.
8. The following table gives the distribution of the lifetime of 400 neon lamps:
| Lifetime (in hours) | Number of lamps |
| 1500 – 2000 | 14 |
| 2000 – 2500 | 56 |
| 2500 – 3000 | 60 |
| 3000 – 3500 | 86 |
| 3500 – 4000 | 74 |
| 4000 – 4500 | 62 |
| 4500 – 5000 | 48 |
Find the median life.
Solution:
| Lifetime | Number of lamps fi | Cumulative frequency (cf) |
| 1500 – 2000 | 14 | 14 |
| 2000 – 2500 | 56 | 70 |
| 2500 – 3000 | 60 | 130(F) |
| 3000 – 3500 | 86(f) | 216 |
| 3500 – 4000 | 74 | 290 |
| 4000 – 4500 | 62 | 352 |
| 4500 – 5000 | 48 | 400 |
| N = 400 |
It’s seen that the cumulative frequency just greater than n/2 (400/2 = 200) is 216, and it belongs to the class interval 3000 – 3500, which becomes the Median class = 3000 – 3500
Lower limits (l) of median class = 3000 and,
Frequency (f) of median class = 86
Cumulative frequency (cf) of class preceding median class = 130
And the Class size (h) = 500
Thus, by calculating the median by the formula, we get

= 3000 + (35000/86)
= 3406.98
Thus, the median lifetime of lamps is 3406.98 hours.
9. The distribution below gives the weight of 30 students in a class. Find the median weight of students.
| Weight (in kg): | 40 – 45 | 45 – 50 | 50 – 55 | 55 – 60 | 60 – 65 | 65 – 70 | 70 – 75 |
| No of students: | 2 | 3 | 8 | 6 | 6 | 3 | 2 |
Solution:
| Weight (in kg) | Number of students fi | Cumulative frequency (cf) |
| 40 – 45 | 2 | 2 |
| 45 – 50 | 3 | 5 |
| 50 – 55 | 8 | 13 |
| 55 – 60 | 6 | 19 |
| 60 – 65 | 6 | 25 |
| 65 – 70 | 3 | 28 |
| 70 – 75 | 2 | 30 |
It’s seen that the cumulative frequency just greater than n/ 2 (i.e. 30/ 2 = 15) is 19, belongs to class interval 55 – 60.
So, it’s chosen that
Median class = 55 – 60
Lower limit (l) of median class = 55
Frequency (f) of median class = 6
Cumulative frequency (cf) = 13
And, Class size (h) = 5
Thus, by calculating the median by the formula, we get

= 55 + 10/6 = 56.666
So, the median weight is 56.67 kg.
10. Find the missing frequencies and the median for the following distribution if the mean is 1.46
| No. of accidents | 0 | 1 | 2 | 3 | 4 | 5 | Total |
| Frequencies (no. of days) | 46 | ? | ? | 25 | 10 | 5 | 200 |
Solution:
| No. of accidents (x) | No. of days (f) | fx |
| 0 | 46 | 0 |
| 1 | x | x |
| 2 | y | 2y |
| 3 | 25 | 75 |
| 4 | 10 | 40 |
| 5 | 5 | 25 |
| N = 200 | Sum = x + 2y + 140 |
It’s given that N = 200
⇒ 46 + x + y + 25 + 10 + 5 = 200
⇒ x + y = 200 – 46 – 25 – 10 – 5
⇒ x + y = 114 —- (i)
And also given, Mean = 1.46
⇒ Sum/ N = 1.46
⇒ (x + 2y + 140)/ 200 = 1.46
⇒ x + 2y = 292 – 140
⇒ x + 2y = 152 —- (ii)
Subtract equation (i) from equation (ii), and we get
x + 2y – x – y = 152 – 114
⇒ y = 38
Now, on putting the value of y in equation (i), we find x = 114 – 38 = 76
Thus, the table becomes
| No. of accidents (x) | No. of days (f) | Cumulative frequency |
| 0 | 46 | 46 |
| 1 | 76 | 122 |
| 2 | 38 | 160 |
| 3 | 25 | 185 |
| 4 | 10 | 195 |
| 5 | 5 | 200 |
| N = 200 |
It’s seen that,
N = 200 N/2 = 200/2 = 100
So, the cumulative frequency is more than N/2 is 122
Therefore, the median is 1.
RD Sharma Solutions for Class 10 Maths Chapter 7 Exercise 7.5 Page No: 7.34
1. Find the mode of the following data:
(i) 3, 5, 7, 4, 5, 3, 5, 6, 8, 9, 5, 3, 5, 3, 6, 9, 7, 4
(ii) 3, 3, 7, 4, 5, 3, 5, 6, 8, 9, 5, 3, 5, 3, 6, 9, 7, 4
(iii) 15, 8, 26, 25, 24, 15, 18, 20, 24, 15, 19, 15
Solution:
(i)
| Value (x) | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Frequency (f) | 4 | 2 | 5 | 2 | 2 | 1 | 2 |
Thus, the mode = 5 since it occurs the maximum number of times.
(ii)
| Value (x) | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Frequency (f) | 5 | 2 | 4 | 2 | 2 | 1 | 2 |
Thus, the mode = 3 since it occurs the maximum number of times.
(iii)
| Value (x) | 8 | 15 | 18 | 19 | 20 | 24 | 25 |
| Frequency (f) | 1 | 4 | 1 | 1 | 1 | 2 | 1 |
Thus, the mode = 15 since it occurs the maximum number of times.
2. The shirt size worn by a group of 200 persons, who bought the shirt from a store, are as follows:
| Shirt size | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
| Number of persons | 15 | 25 | 39 | 41 | 36 | 17 | 15 | 12 |
Find the model shirt size worn by the group.
Solution:
| Shirt size | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
| Number of persons | 15 | 25 | 39 | 41 | 36 | 17 | 15 | 12 |
From the data, it’s observed that
Model shirt size = 40 since it was the size which occurred for the maximum number of times.
3. Find the mode of the following distribution.
(i)
| Class interval | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 | 70 – 80 |
| Frequency | 5 | 8 | 7 | 12 | 28 | 20 | 10 | 10 |
Solution:
| Class interval | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 | 70 – 80 |
| Frequency | 5 | 8 | 7 | 12 | 28 | 20 | 10 | 10 |
It’s seen that the maximum frequency is 28.
So, the corresponding class, i.e., 40 – 50 is the modal class.
And,
l = 40, h = 50 40 = 10, f = 28, f1 = 12, f2 = 20
Using the formula for finding mode, we get

= 40 + 160/ 24
= 40 + 6.67
= 46.67
(ii)
| Class interval | 10 – 15 | 15 – 20 | 20 – 25 | 25 – 30 | 30 – 35 | 35 – 40 |
| Frequency | 30 | 45 | 75 | 35 | 25 | 15 |
Solution:
| Class interval | 10 – 15 | 15 – 20 | 20 – 25 | 25 – 30 | 30 – 35 | 35 – 40 |
| Frequency | 30 | 45 | 75 | 35 | 25 | 15 |
It’s seen that the maximum frequency is 75.
So, the corresponding class, i.e., 20 – 25 is the modal class.
And,
l = 20, h = 25 – 20 = 5, f = 75, f1 = 45, f2 = 35
Using the formula for finding mode, we get

= 20 + 150/70
= 20 + 2.14
= 22.14
(iii)
| Class interval | 25 – 30 | 30 – 35 | 35 – 40 | 40 – 45 | 45 – 50 | 50 – 55 |
| Frequency | 25 | 34 | 50 | 42 | 38 | 14 |
Solution:
| Class interval | 25 – 30 | 30 – 35 | 35 – 40 | 40 – 45 | 45 – 50 | 50 – 55 |
| Frequency | 25 | 34 | 50 | 42 | 38 | 14 |
It’s seen that the maximum frequency is 50.
So, the corresponding class, i.e., 35 – 40 is the modal class.
And,
l = 35, h = 40 – 35 = 5, f = 50, f1 = 34, f2 = 42
Using the formula for finding mode, we get

= 35 + 80/24
= 35 + 3.33
= 38.33
4. Compare the modal ages of two groups of students appearing for an entrance test.
| Age in years | 16 – 18 | 18 – 20 | 20 – 22 | 22 – 24 | 24 – 26 |
| Group A | 50 | 78 | 46 | 28 | 23 |
| Group B | 54 | 89 | 40 | 25 | 17 |
Solution:
| Age in years | 16 – 18 | 18 – 20 | 20 – 22 | 22 – 24 | 24 – 26 |
| Group A | 50 | 78 | 46 | 28 | 23 |
| Group B | 54 | 89 | 40 | 25 | 17 |
For Group A:
It’s seen that the maximum frequency is 78.
So, the corresponding class 18 – 20 is the model class.
And,
l = 18, h = 20 – 18 = 2, f = 78, f1 = 50, f2 = 46
Using the formula for finding mode, we get

= 18 + 56/60
= 18 + 0.93
= 18.93 years
For group B:
It’s seen that the maximum frequency is 89.
So, the corresponding class 18 – 20 is the modal class.
And,
l = 18, h = 20 – 18 = 2, f = 89, f1 = 54, f2 = 40
Using the formula for finding mode, we get

Mode
= 18 + 70/84
= 18 + 0.83
= 18.83 years
Therefore, the modal age of Group A is higher than that of Group B.
5. The marks in science for 80 students of Class X are given below. Find the mode of the marks obtained by the students in science.
| Marks | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 | 70 – 80 | 80 – 90 | 90 – 100 |
| Frequency | 3 | 5 | 16 | 12 | 13 | 20 | 5 | 4 | 1 | 1 |
Solution:
| Marks | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 | 70 – 80 | 80 – 90 | 90 – 100 |
| Frequency | 3 | 5 | 16 | 12 | 13 | 20 | 5 | 4 | 1 | 1 |
It’s seen that the maximum frequency is 20.
So, the corresponding class 50 – 60 is the modal class.
And,
l = 50, h = 60 – 50 = 10, f = 20, f1 = 13, f2 = 5
Using the formula for finding mode, we get

= 50 + 70/22
= 50 + 3.18
= 53.18
6. The following is the distribution of height of students of a certain class in a city:
| Height (in cm): | 160 – 162 | 163 – 165 | 166 – 168 | 169 – 171 | 172 – 174 |
| No of students: | 15 | 118 | 142 | 127 | 18 |
Find the average height of the maximum number of students.
Solution:
| Heights (exclusive) | 160 – 162 | 163 – 165 | 166 – 168 | 169 – 171 | 172 – 174 |
| Heights (inclusive) | 159.5 – 162.5 | 162.5 – 165.5 | 165.5 – 168.5 | 168.5 – 171.5 | 171.5 – 174.5 |
| No. of students | 15 | 118 | 142 | 127 | 18 |
It’s seen that the maximum frequency is 142.
So, the corresponding class 165.5 – 168.5 is the modal class.
And,
l = 165.5, h = 168.5 – 165.5 = 3, f = 142, f1 = 118, f2 = 127
Using the formula for finding mode, we get

= 165.5 + 72/39
= 165.5 + 1.85
= 167.35 cm
7. The following table shows the ages of the patients admitted to a hospital during a year:
| Ages (in years) | 5 – 15 | 15 – 25 | 25 – 35 | 35 – 45 | 45 – 55 | 55 – 65 |
| No of students | 6 | 11 | 21 | 23 | 14 | 5 |
Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency.
Solution:
To find the mean:
For the given data, let the assumed mean (A) = 30
| Age (in years) | Number of patients fi | Classmarks xi | di = xi – 275 | fidi |
| 5 – 15 | 6 | 10 | – 20 | -120 |
| 15 – 25 | 11 | 20 | – 10 | -110 |
| 25 – 35 | 21 | 30 | 0 | 0 |
| 35 – 45 | 23 | 40 | 10 | 230 |
| 45 – 55 | 14 | 50 | 20 | 280 |
| 55 – 65 | 5 | 60 | 30 | 150 |
| N = 80 | Σfi di = 430 |
It’s observed from the table that Σfi = N = 80 and Σfi di = 430.
Using the formula for mean,

= 30 + 430/80
= 30 + 5.375
= 35.375
= 35.38
Thus, the mean of this data is 35.38. It can also be interpreted as that, on an average, the age of patients admitted to the hospital was 35.38 years.
It is also observed that the maximum class frequency is 23, and it belongs to the class interval 35 – 45
So, the modal class is 35 – 45 with the Lower limit (l) of modal class = 35
And, Frequency (f) of modal class = 23
Class size (h) = 10
Frequency (f1) of class preceding the modal class = 21
Frequency (f2) of class succeeding the modal class = 14

Mode
Therefore, the mode is 36.8. This represents that the maximum number of patients admitted to the hospital was of 36.8 years.
Hence, it’s seen that mode is greater than the mean.
8. The following data gives information on the observed lifetimes (in hours) of 225 electrical components:
| Lifetimes (in hours) | 0 – 20 | 20 – 40 | 40 – 60 | 60 – 80 | 80 – 100 | 100 – 120 |
| No. of components | 10 | 35 | 52 | 61 | 38 | 29 |
Determine the modal lifetimes of the components.
Solution:
From the data given above, it’s observed that the maximum class frequency is 61, which belongs to the class interval 60 – 80.
So, modal class limit (l) of modal class = 60
Frequency (f) of modal class = 61
Frequency (f1) of class preceding the modal class = 52
Frequency (f2) of class succeeding the modal class = 38
Class size (h) = 20
Using the formula for find mode, we have

Mode
Thus, the modal lifetime of electrical components is 65.625 hours.
9. The following table gives the daily income of 50 workers of a factory:
| Daily income | 100 – 120 | 120 – 140 | 140 – 160 | 160 – 180 | 180 – 200 |
| Number of workers | 12 | 14 | 8 | 6 | 10 |
Find the mean, mode and median of the above data.
Solution:
| Class interval | Mid value (x) | Frequency (f) | fx | Cumulative frequency |
| 100 – 120 | 110 | 12 | 1320 | 12 |
| 120 – 140 | 130 | 14 | 1820 | 26 |
| 140 – 160 | 150 | 8 | 1200 | 34 |
| 160 – 180 | 170 | 6 | 1000 | 40 |
| 180 – 200 | 190 | 10 | 1900 | 50 |
| N = 50 | Σfx = 7260 |
We know that,
Mean = Σfx / N
= 7260/ 50
= 145.2
Then,
We have, N = 50
⇒ N/2 = 50/2 = 25
So, the cumulative frequency just greater than N/2 is 26, then the median class is 120 – 140.
Such that l = 120, h = 140 – 120 = 20, f = 14, F = 12

= 120 + 260/14
= 120 + 18.57
= 138.57
From the data, it’s observed that the maximum frequency is 14, so the corresponding class 120 – 140 is the modal class.
And,
l = 120, h = 140 – 120 = 20, f = 14, f1 = 12, f2 = 8

= 120 + 5
= 125
Therefore, mean = 145.2, median = 138.57 and mode = 125
RD Sharma Solutions for Class 10 Maths Chapter 7 Exercise 7.6 Page No: 7.62
1. Draw an ogive by less than the method for the following data.
| No. of rooms | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| No. of houses | 4 | 9 | 22 | 28 | 24 | 12 | 8 | 6 | 5 | 2 |
Solution:
| No. of rooms | No. of houses | Cumulative Frequency |
| Less than or equal to 1 | 4 | 4 |
| Less than or equal to 2 | 9 | 13 |
| Less than or equal to 3 | 22 | 35 |
| Less than or equal to 4 | 28 | 63 |
| Less than or equal to 5 | 24 | 87 |
| Less than or equal to 6 | 12 | 99 |
| Less than or equal to 7 | 8 | 107 |
| Less than or equal to 8 | 6 | 113 |
| Less than or equal to 9 | 5 | 118 |
| Less than or equal to 10 | 2 | 120 |
It’s required to plot the points (1, 4), (2, 13), (3, 35), (4, 63), (5, 87), (6, 99), (7, 107), (8, 113), (9, 118), (10, 120), by taking upper-class limit over the x-axis and cumulative frequency over the y-axis.

2. The marks scored by 750 students in an examination are given in the form of a frequency distribution table.
| Marks | No. of Students |
| 600 – 640 | 16 |
| 640 – 680 | 45 |
| 680 – 720 | 156 |
| 720 – 760 | 284 |
| 760 – 800 | 172 |
| 800 – 840 | 59 |
| 840 – 880 | 18 |
Prepare a cumulative frequency distribution table by less than method and draw an ogive.
Solution:
| Marks | No. of Students | Marks Less than | Cumulative Frequency |
| 600 – 640 | 16 | 640 | 16 |
| 640 – 680 | 45 | 680 | 61 |
| 680 – 720 | 156 | 720 | 217 |
| 720 – 760 | 284 | 760 | 501 |
| 760 – 800 | 172 | 800 | 673 |
| 800 – 840 | 59 | 840 | 732 |
| 840 – 880 | 18 | 880 | 750 |
Plot the points (640, 16), (680, 61), (720, 217), (760, 501), (800, 673), (840, 732), (880, 750) by taking upper-class limit over the x-axis and cumulative frequency over the y-axis.

3. Draw an Ogive to represent the following frequency distribution.
| Class-interval | 0 – 4 | 5 – 9 | 10 – 14 | 15 – 19 | 20 – 24 |
| No. of students | 2 | 6 | 10 | 5 | 3 |
Solution:
Since the given frequency distribution is not continuous, we will have to first make it continuous and then prepare the cumulative frequency.
| Class interval | No. of Students | Less than | Cumulative frequency |
| 0.5 – 4.5 | 2 | 4.5 | 2 |
| 4.5 – 9.5 | 6 | 9.5 | 8 |
| 9.5 – 14.5 | 10 | 14.5 | 18 |
| 14.5 – 19.5 | 5 | 19.5 | 23 |
| 19.5 – 24.5 | 3 | 24.5 | 26 |
Plot the points (4.5, 2), (9.5, 8), (14.5, 18), (19.5, 23), (24.5, 26) by taking the upper-class limit over the x-axis and cumulative frequency over the y-axis.

4. The monthly profits (in Rs) of 100 shops are distributed as follows:
| Profit per shop | No of shops: |
| 0 – 50 | 12 |
| 50 – 100 | 18 |
| 100 – 150 | 27 |
| 150 – 200 | 20 |
| 200 – 250 | 17 |
| 250 – 300 | 6 |
Draw the frequency polygon for it.
Solution:
Doing for the less than method, we have
| Profit per shop | Mid-value | No. of shops |
| Less than 0 | 0 | 0 |
| Less than 0 – 50 | 25 | 12 |
| Less than 50 – 100 | 75 | 18 |
| Less than 100 – 150 | 125 | 27 |
| Less than 150 – 200 | 175 | 20 |
| Less than 200 – 250 | 225 | 17 |
| Less than 250 – 300 | 275 | 6 |
| Above 300 | 300 | 0 |
By plotting the respective coordinates, we can get the frequency polygon.

5. The following distribution gives the daily income of 50 workers of a factory:
| Daily income (in Rs): | No of workers: |
| 100 – 120 | 12 |
| 120 – 140 | 14 |
| 140 – 160 | 8 |
| 160 – 180 | 6 |
| 180 – 200 | 10 |
Convert the above distribution to a ‘less than’ type cumulative frequency distribution and draw its ogive.
Solution:
Firstly, we prepare the cumulative frequency table by less than method as given below.
| Daily income | Cumulative frequency |
| Less than 120 | 12 |
| Less than 140 | 26 |
| Less than 160 | 34 |
| Less than 180 | 40 |
| Less than 200 | 50 |
Now, we mark on the x-axis upper-class limit and y-axis cumulative frequencies. Thus, we plot point (120, 12), (140, 26), (160, 34), (180, 40), (200, 50).







































Comments