As a continuation of your previous Class, students are now introduced to the construction of several other geometrical figures and also given their justification. This exercise deals with problems in understanding and constructing the division of a line segment. Students can refer to the RD Sharma Solutions Class 10 to get a clear idea of how the answers are to be presented in their exams. Further, students can also download the RD Sharma Solutions for Class 10 Maths Chapter 11 Constructions Exercise 11.1 PDF provided below for reference.
RD Sharma Solutions for Class 10 Maths Chapter 11 Constructions Exercise 11.1 Download PDF
Access answers to Maths RD Sharma Solutions for Class 10 Chapter 11 Constructions Exercise 11.1
1. Determine a point which divides a line segment of length 12 cm internally in the ratio of 2: 3. Also, justify your construction.
Solution:
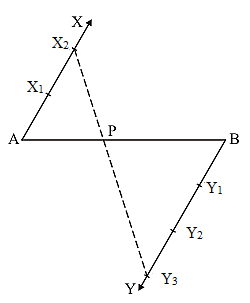
Steps of construction:
1. Draw a line segment AB = 12 cm by using a ruler.
2. Through points A and B, draw two parallel lines on the opposite side of AB and make the same acute angles with the line segment.
3. Cut 2 equal parts on AX and 3 equal parts on BY such that AX1 = X1X2 and BY1 = Y1Y2 = Y2Y3.
4. Join X2Y3, which intersects AB at P
Hence, AP/PB = 2/3.
Justification:
In ΔAX2P and ΔBY3P, we have
∠APX2 = ∠BPY3 [vertically opposite angle]
∠X2AP = ∠Y3BP [alternate interior angles}
ΔAX2P = ΔBY3P [Because AA similarity]
∴ AP/BP = AX2/BY3 = 2/3 [From C.P.C.T]

Comments