Word problems based on mixture and alligation are asked in the quantitative aptitude section of the various Government exams.
Mostly the number of questions asked from this section varies between 1-3 and are a bit tricky to solve. Aspirants preparing for the upcoming Government exams must practise well to be able to answer questions from this topic.
Candidates can also check the detailed quantitative aptitude syllabus and the exams in which this section is included at the linked article.
| Table of Contents: |
In this article, we bring to you the detailed concept of mixture and alligation, along with some important formulas to solve questions based on this topic. We shall also discuss some tips which will make the solution simpler and explain the same with the help of some sample examples.
It must be ensured that since there is sectional cut off in almost all competitive exams, it is important that equal attention is paid on the preparation of each subject.
Given below are a few quantitative aptitude concept links for your assistance:
| Data Interpretation | Boat and Stream | Data Sufficiency |
| Number Series | Pipes and Cistern Questions | Approximation and Simplification |
Mixture & Alligation Questions PDF:-Download PDF Here

Mixture and Alligation – Concept
A mixture, as the name suggests is mixing two or more things together and alligation enables us to find the ratio in which the ingredients/ things have been mixed and at what price they are sole to earn profit or face loss.

To solve mixture and alligation questions, one must know that alligation is used to find the mean value of a mixture when the ratio and amount of the ingredients mixed are different and also to find the proportion in which the elements are mixed.
It may sound a bit complex but once the candidate solves questions based on the same, the concept becomes clearer.
Aspirants can check the links given below to prepare themselves even better for the upcoming competitive exams:
| Problems on Age | Problems on Train | Important Maths Questions for SBI PO |
| Tips to Solve Quadratic Equations | Logical Reasoning | General English for Competitive Exams |
Important Formulas for Mixture and Alligation
To solve any numerical ability question, candidates need to know a set of formulas for each topic which make solving the questions easier and time-saving. This, given below are a few formulas which will help candidates with the same and let them solve the mixture and alligation questions more conveniently:
- The basic formula which is used to find the ratio in which the ingredients are mixed is
![]()
It is also called the rule of alligation and can also be represented as
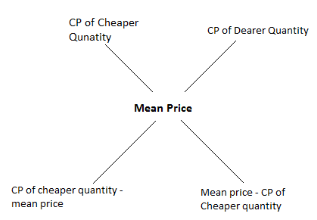
Candidates who are looking forward to applying for the upcoming Government exams and wish to solve more and more question papers and mock tests to speed up their calculation skills and enhance their preparation can refer to the links given below:
- Free Online Government Exam Quiz
- Previous Year Government Exam Question Papers PDF with Solutions
- Bank PO Question Papers with Solutions
- Free Online Mock Tests with Solutions
Tips and Tricks To Solve Questions
Time management plays a very important role in the Government exams and candidates cannot afford to lose much time while solving any of the given questions. Thus, a few simple tricks and tips will also prove to be helpful for the candidates to solve the mixture alligation questions easily:
- The rule of alligation can also be used to solve questions based partnerships, time and work and wages
- Read a question and try placing the values in the alligation rule mentioned above to solve the question
- Questions from this topic may sound a bit tricky but are easy to solve if once a candidate get familiar with the concept and the important formulas used
- You can not just find the ratio between the quantity of two elements but also the rate at which the article can be sold using the alligation rule
Any tip will only be useful if a candidate spends quality time practising the mixture and alligation questions and apply the rule of alligation to find answers for the same.
Get maths tricks and shortcut to solve the quantitative aptitude questions more efficiently and easily.
Candidates who wish to perform even better must visit the links given below to analyse the syllabus for each Government sector exam:
| Bank Exam Syllabus | SSC Syllabus | RRB Syllabus |
| LIC Syllabus | Verbal Ability | UPSC CAPF Syllabus |
Mixture and Alligation Questions
Below we have discussed a few mixture and alligation based questions for your reference and to help you assist in understanding the concept and applying the formula effectively to solve the questions.
Q 1. A grocer wishes to sell a mixture of two variety of pulses worth Rs.16 per kg. In what ratio must he mix the pulses to reach this selling price, when cost of one variety of pulses is Rs.14 per kg and the other is Rs.24 per kg?
- 2:5
- 4:3
- 2:1
- 4:1
- 7:6
Answer: (4) 4:1
Solution:
Using the rule of alligation,

⇒ 8:2 = 4:1
Q 2. Cost of two types of pulses is Rs.15 and Rs, 20 per kg, respectively. If both the pulses are mixed together in the ratio 2:3, then what should be the price of mixed variety of pulses per kg?
- Rs. 22 per kg
- Rs. 30 per kg
- Rs. 10 per kg
- Rs. 18 per kg
- Rs. 24 per kg
Answer: (4) Rs. 18 per kg
Solution:
Let the cost of mixed variety of pulse be Rs. x
As per the alligation rule,
2:3 = (20-x) : (x-15)
⇒ 2x+3x = 60+30
⇒ 5x = 90
⇒ x = 18
Q 3. A dealer has 1000 kg sugar and he sells a part of it at 8% profit and the rest of it at 18% profit. The overall profit he earns is 14%. What is the quantity which is sold at 18% profit?
- 250 kg
- 600 kg
- 620 kg
- 400 kg
- 450 kg
Answer: (2) 600 kg
Solution:
As per the rule of alligation,
Quantity of Dearer: Quantity of Cheaper = (18-14) : (14-8) = 4:6 = 2:3
Quantity of sugar sold at 18% profit = 3/5 × 1000 = 600kg
Q 4. How much coffee of variety A, costing Rs. 5 a kg should be added to 20 kg of Type B coffee at Rs. 12 a kg so that the cost of the two coffee variety mixture be worth Rs. 7 a kg?
- 25 kg
- 34 kg
- 55 kg
- 52 kg
- 50 kg
Answer: (5) 50 kg
Solution:
As per the rule of alligation,
Quantity of Dearer: Quantity of Cheaper = (12-7) : (7-5) = 5:2
Quantity of Variety A coffee that needs to be mixed ⇒ 5:2 = x:20
⇒ x =50 kg
The above-given questions are just a sample mixture and alligation questions. Candidates must solve more of these to get a better understanding of the topic.
Mixture & Alligation Questions PDF:-Download PDF Here
Aspirants can also check the related preparation links given below to ace the upcoming Government exams:
Candidates looking for Government exam updates, information, study material or preparation tips can refer to BYJU’S for assistance.
Refer to the following video to get the continued explanation and analysis of the Mixture and Alligation concept:


I really appreciate you work of teaching