In trigonometry, Sine, Cosine and Tangent are the three major or primary ratios, which are used to find the angles and length of the sides of the triangle. Before determining Cos 60 degrees whose value is equal to 1/2, let us know the importance of Cosine function in trigonometry.
Cosine function defines a relation between the adjacent side and the hypotenuse of a right triangle with respect to the angle formed between the adjacent side and the hypotenuse. In other words, the Cosine of angle α is equal to the ratio of the adjacent side (also called as a base) and hypotenuse of a right-angled triangle.
Also, find a few important values of other trigonometric ratios:
- Tan 60 degrees
- Tan 30 degrees
- Sin 30 degrees
- Cos 30 degrees
- Cos 0 degrees
- Sin 60 degrees
The trigonometric functions, sin, cos and tan for an angle are the primary functions. The value for cos 60 degrees and other trigonometry ratios for all the degrees 0°, 30°, 45°, 90°, 180° are generally used in trigonometry equations. These trigonometric values are easy to memorize with the help trigonometry table.
Cos 60 Degree Value
In a right-angled triangle, the cosine of ∠α is a ratio of the length of the adjacent side (base) to the ∠α and its hypotenuse, where ∠α is the angle formed between the adjacent side and the hypotenuse.

Cosine α = Adjacent Side / Hypotenuse
Cos α = AC / AB
Cos α = b / h
Now, to find the value of cos 60 degrees, let us consider, an equilateral triangle ABC as given below:

Here, AB = BC = AC and AD is perpendicular bisecting BC into two equal parts.
As we know, cos B = BD/AB
Let us consider the length of each side as 2 units, such as AB = BC = AC = 2 units and BD = CD = 1 unit.
Therefore, the value of cos 60° = BD/AB = ½
In the same way, we can write the value of sin 60° and tan 60° by evaluating the required sides.
In right triangle ABD, by Pythagoras theorem:
AB2 = AD2+ BD2
22 = AD2 + 12
AD2 = 22 -12
AD2 = 4 – 1
AD2 = 3
AD = √3
Now, we have got all the sides of triangle ABD.
Sin 60° = AD/AB = √3/2
Tan 60° = AD/BD = √3 / 1 = √3
We can also write the value of cos 60 degrees in decimal form as:
cos 60° = 1/2 = 0.5
Also, we can write the values of sine, cosine and tangent with respect to all the degrees in a table.
Let us draw a table with respect to degrees and radians for sine, cosine and tangent functions.
| Angle in Degrees | 0 | 30 | 45 | 60 | 90 | 180 | 270 | 360 |
| Angle in Radians | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| Sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| Cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| Tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
Unit Circle in Trigonometry
It is possible to give the values of trigonometric ratios with respect to radians equivalent to degrees, in case of a unit circle, whose radius is equal to one. The radian for a unit circle is denoted by π. In the below figure, the angle values are represented in degrees instead of radians.
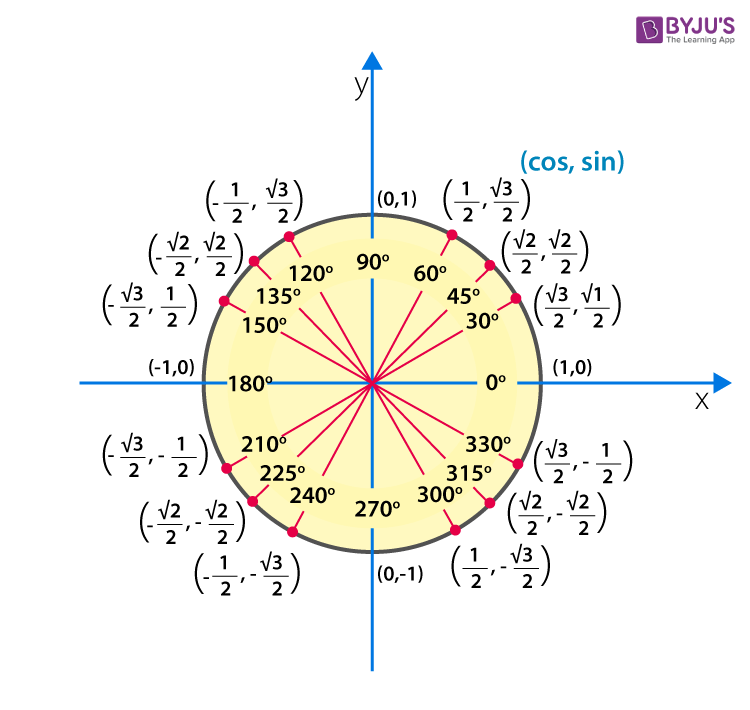
You have learned about cos 60 degrees value along with other degree’s values here now. Also, the derived values for sin and tan with respect to degrees and radians. In the same way, we can find the values for other trigonometric ratios like secant, cosecant and cotangent.
Let us see some example where we can use the value of cos 60 degrees.
Example 1: Find the value of cos 60° + sin 30°.
Solution:
cos 60° + sin 30°
= cos 60° + sin (90° – 60°)
= cos 60° + cos 60°
= (1/2) + (1/2)
= (1 + 1)/2
= 2/2
= 1
Alternatively, cos 60° + sin 30° = (1/2) + (1/2) = (1 + 1)/2 = 2/2 = 1
Example 2: Calculate: 2 sin 60° – 4 cos 60°
Solution:
We know that, sin 60° = √3/2 and cos 60° = 1/2
Thus, 2 sin 60° – 4 cos 60° = 2(√3/2) – 4(1/2)
= √3 – 2
Learn more about trigonometric ratios/identities/functions at BYJU’S and download BYJU’S – The Learning App for a better experience.
| MATHS Related Links | |
| Cosine Rule | Inverse Cosine |
| Law of Cosines | Trigonometric Equations |


thanks it helped me alot