The value of tan 30 degrees is 1/√3. The value of tan π/6 can be evaluated with the help of a unit circle, graphically. In trigonometry, the tangent of an angle in a right-angled triangle is equal to the ratio of opposite side and the adjacent side of the angle.
Tan 30 degrees is also represented by tan π/6 in terms of radians. The exact value of tan 30° is 0.57735.
| Tan 30° = 1/√3 = 0.57735 |
The value of tangent of angle 30 degrees can also be evaluated using the values of sin 30 degrees and cos 30 degrees. Let us learn in detail in this article.
Tan 30 Degrees Value
Tangent 30 degrees value is one by root 3 (1/√3). Like Sine and Cosine, Tangent is also a basic function of trigonometry. Most of the trigonometric equation is based on these ratios. Usually, to find the values of sine, cosine and tangent ratios, we use right-angles triangle and also take a unit circle example. First, let us discuss tan 30 degrees value in terms of a right-angled triangle.
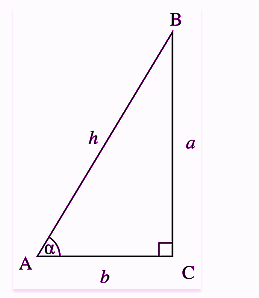
Suppose for a triangle ABC, right-angled at C, α is the angle, h is the hypotenuse, b is the adjacent side or base and a is the opposite side or perpendicular. As we know,
Tan α =Opposite Side/Adjacent Side
∴ Tan α=a/b
Similarly, we can also find the value for Sine and Cosine ratios.
Sin α= Opposite Side/Hypotenuse
∴ Sin α =a/h
And
Cos α = [Adjacent Side/Hypotenuse]
∴ Cos α = b/h
Find Tan 30 Value Using Sin and Cos Function
We can also represent the tangent function as the ratio of the sine function and cosine function.
∴ Tan α = sin α/cos α
So, tan 30 degrees we can write as;
Tan 30°=sin 30°/cos 30°
We know,
Sin 30° = 1/2 & Cos 30° = √3/2
∴ Tan 30° = (1/2) /(√3/2)
Tan 30° = 1/√3
Hence, the value of Tan 30 degrees is 1/√3
We can also find the value of tan 0, tan 45, tan 60 and tan 90 in the same manner.
Tan 0 = sin 0/cos 0 = 0/1 = 0
Tan 45 = sin 45/cos 45 = (1/√2)/(1/√2) = 1
Tan 60 = sin 60/cos 60 = (√3/2)/(½) = √3
Tan 90 = sin 90/cos 90 = 1/0 = Not defined
Unit Circle Tangent
Unit Circle: For a unit circle also we can calculate the value of tan 30 degrees. The unit circle has a radius as 1 unit and it is drawn on an XY plane. With the below graph, you can check the values of all the trigonometry ratios, such as sin, cos, tan, sec, cot and cosec.
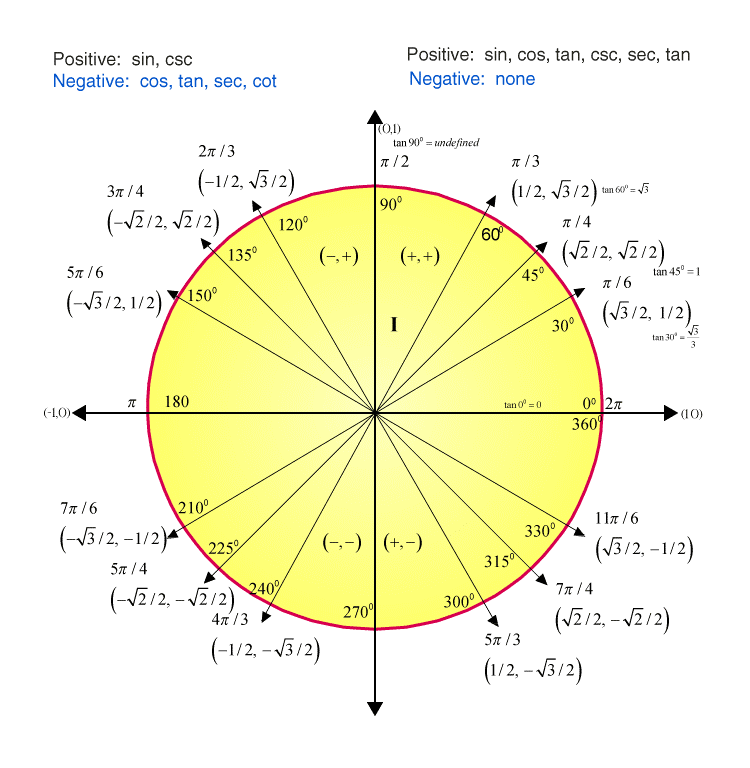
Also, you can see, the values are defined here in terms of radians in case of the unit circle and not in degrees. In the same way, we can derive other values of tangent degrees(0°,45°,60°,90°,180°,270° and 360°).
Important Angles of Tan (30, 45, 60)
In trigonometry, when we learn about the ratio of angles, the three primary ratios are sine, cosine and tangent. Also, we learn these ratios in terms of angles, such as 0°, 30°, 45°, 60° and 90°.
Among these angles 30, 45 and 60 degrees are important to remember. Also, learn them in terms of radians.
Tan 30 = Tan π/6 = 1/√3
Tan 45 = Tan π/4 = 1
Tan 60 = Tan π/3 = √3
Tan 0 = 0 and tan 90 = Not defined, are easy to remember.
Check the below trigonometry table to get the values for all trigonometry ratios.
| Angle
Radian |
0°
0 |
30°
π/6 |
45°
π/4 |
60°
π/3 |
90°
π/2 |
180°
π |
270°
3π/2 |
360°
2π |
| Sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| Cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| Tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| Cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| Sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
| Cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
Trigonometry Formulas Based on Tangent Function
- Tan (-θ)=-Tan θ
- Tan (x+y)=(tan x +tan y)/(1-tan x tan y)
- Tan (x-y)=(tan x -tan y)/(1+tan x tan y)
- Tan 2x=2 tan x/1-tan2 x
- Tan 3x= 3tan x-tan3 x/1-3 tan2 x
- Tan (90-θ)=Cot θ
- Tan (90+θ)= -Cot θ
Keep learning with us and Download BYJU’S -The learning app for interactive videos.
| MATHS Related Links | |
| Tan 0 Degree | Trigonometric Identities |
| Tan 60 Degree | Tan 90 Degree |
Frequently Asked Questions – FAQs
What is the exact value of tan 30 degrees?
How to find the value of tan π/6?
Tan π/6 = (sin π/6)/(cos π/6)
Since, we know, sin π/6 = ½ and cos π/6 = √3/2
By putting the value of sin π/6 and cos π/6 we get;
Tan π/6 = (½)/(√3/2) = 1/√3
What is the value of tan 90?
Is the value of tan 0 and sin 0 equal?
Also remember, tan 0 = sin = cos 90. It implies that in a unit circle, when the value of tan and sine ratio is equal to 0 then the value of cos will be 1.


Comments