The first exercise of this chapter provides the basic knowledge regarding the representation of linear equations graphically and algebraically. We know the geometric representation of a linear equation in two variables is a straight line. The RD Sharma Solutions Class 10 explains further key concepts regarding this and other chapters vital for students’ preparation for exams. Students can access the RD Sharma Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.1 PDF given below.
RD Sharma Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.1
Access RD Sharma Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.1
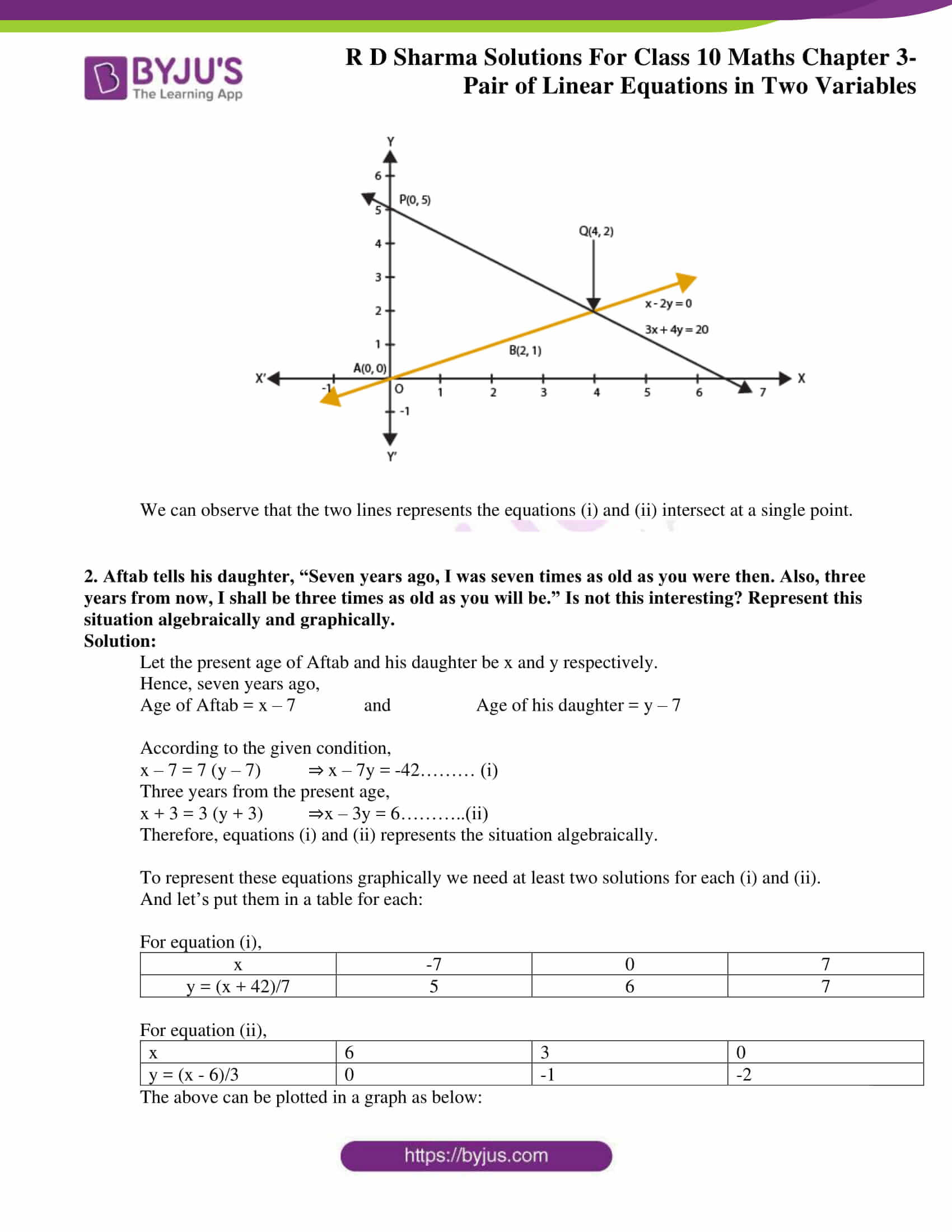
1. Akhila went to a fair in her village. She wanted to enjoy rides on the Giant Wheel and play Hoopla (a game in which you throw a rig on the items in the stall, and if the ring covers any object completely you get it). The number of times she played Hoopla is half the number of rides she had on the giant wheel. Each ride costs ₹3 and a game of hoopla costs ₹4. If she spent ₹20 in the fair, represent this situation algebraically and graphically.
Solution:
Let ‘x’ be the number of rides Akhila had on the giant wheel.
And, let ‘y’ be the number of times she played Hoopla.
From the question we can write the below pair of equations.
y = (1/2)x ⇒ x -2y = 0……. (i)
3x + 4y = 20……. (ii)
To represent these equations graphically, we need at least two solutions for each (i) and (ii).
And let’s put them in a table for each:
For equation (i),
| x | 0 | 2 |
| y = (1/2)x | 0 | 1 |
For equation (ii),
| x | 0 | 20/3 | 4 |
| y = (20 – 3x)/4 | 5 | 0 | 2 |
When:
The solution of the variable is zero; the equation can be solved easily. Putting x =0 in equation (ii), we get
4y = 20 ⇒y = 5
Similarly putting y = 0 in equation (ii) we get
3x = 20 ⇒x = 20/3 but it is not an integer so it is not easy to plot on graph paper.
So, we chose y=2, which gives x =4 as an integer value.
The above can be plotted in a graph as below:

We can observe that the two lines represents the equations (i) and (ii) intersect at a single point.
2. Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” Is not this interesting? Represent this situation algebraically and graphically.
Solution:
Let the present age of Aftab and his daughter be x and y, respectively.
Hence, seven years ago,
Age of Aftab = x – 7 and Age of his daughter = y – 7
According to the given condition,
x – 7 = 7 (y – 7) ⇒ x – 7y = -42……… (i)
Three years from the present age,
x + 3 = 3 (y + 3) ⇒x – 3y = 6………..(ii)
Therefore, equations (i) and (ii) represent the situation algebraically.
To represent these equations graphically, we need at least two solutions for each (i) and (ii).
And let’s put them in a table for each:
For equation (i),
| x | -7 | 0 | 7 |
| y = (x + 42)/7 | 5 | 6 | 7 |
For equation (ii),
| x | 6 | 3 | 0 |
| y = (x – 6)/3 | 0 | -1 | -2 |
The above can be plotted in a graph as below:

3. The path of the train A is given by the equation 3x+4y-12 =0 and the path of another train B is given by the equation 6x+8y-48 =0. Represent this situation graphically.
Solution:
Given pair of linear equations which represents the paths of train A and train B,
3x + 4y – 12 = 0………………………….. (i)
6x + 8y – 48 = 0 ………………………….. (ii)
To represent these equations graphically, we need at least two solutions for each (i) and (ii).
And let’s put them in a table for each:
For equation (i),
| x | 0 | 4 |
| y = (12 – 3x)/4 | 3 | 0 |
For equation (i),
| x | 0 | 8 |
| y = (48 – 6x)/8 | 6 | 0 |
The above can be plotted in a graph as below:




Comments