The method of cross-multiplication is widely discussed in this exercise. Solving the systems of equations by the method of cross-multiplication is clearly explained in the RD Sharma Solutions Class 10. They are valuable resources developed by experts at BYJU’S for the purpose of clarifying doubts and helping students focus on their weaker areas. Further, students can also make use of the RD Sharma Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.4 PDF given below.
RD Sharma Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.4
Access RD Sharma Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.4
Solve each of the following systems of equations by the method of cross-multiplication:
1. x + 2y + 1 = 0
2x – 3y – 12 = 0
Solution:
The given systems of equations are
x + 2y + 1 = 0
2x – 3y – 12 = 0
For cross-multiplication, we use

Comparing the above two equations with the general form, we get

Hence, the solution for the given system of equations is x = 3 and y = -2.
2. 3x + 2y + 25 = 0
2x + y + 10 = 0
Solution:
The given system of equations is
3x + 2y + 25 = 0
2x + y + 10 = 0
For cross-multiplication, we use

Comparing the above two equations with the general form, we get

Hence, the solution for the given system of equations is x = 5 and y = -20.
3. 2x + y = 35, 3x + 4y = 65
Solution:
The given system of equations can be written as
2x + y – 35 = 0
3x + 4y – 65 = 0
For cross-multiplication, we use,

Comparing the above two equations with the general form, we get

Hence, the solution for the given system of equations is x = 15 and y = 5.
4. 2x – y = 6, x – y = 2
Solution:
The given system of equations can be written as
2x – y – 6 = 0
x – y – 2 = 0
For cross-multiplication, we use

Comparing the above two equations with the general form, we get

Hence, the solution for the given system of equations is x = 4 and y = 2.
5. (x + y)/ xy = 2
(x – y)/ xy = 6
Solution:
The given system of equations is
(x + y)/ xy = 2 ⇒ 1/y + 1/x = 2…….. (i)
(x – y)/ xy = 6 ⇒ 1/y – 1/x = 6……… (ii)
Let 1/x = u and 1/y = v, so the equation becomes
u + y = 2….. (iii)
u – y = 6……(iv)
For cross-multiplication, we use

Comparing the above two equations (iii) & (iv) with the general form, we get

Hence, the solution for the given system of equations is x = -1/2 and y = 1/4.
6. ax + by = a-b
bx – ay = a+b
Solution:
The given system of equations can be written as
ax + by – (a-b) = 0
bx – ay – (a+b) = 0
For cross-multiplication, we use

Comparing the above two equations with the general form, we get

Hence, the solution for the given system of equations is x = 1 and y = -1.
7. x + ay = b
ax + by = c
Solution:
The given system of equations can be written as
x + ay – b = 0
ax + by – c = 0
For cross-multiplication, we use

Comparing the above two equations with the general form, we get

Hence, the solution for the given system of equations is x = (b2 + ac)/(a2 + b2).
and y = (-c2 + ab)/(a2 + b2).
8. ax + by = a2
bx + ay = b2
Solution:
The given system of equations can be written as
ax + by – (a2) = 0
bx + ay – (b2) = 0
For cross-multiplication, we use

Comparing the above two equations with the general form, we get
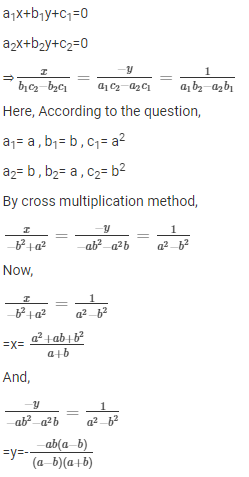
Hence, the solution for the given system of equations is x = (a2 + ab + b2)/(a + b) and y = -ab / (a+ b).
9. 5/(x + y) – 2/(x -y) = -1
15/(x + y) + 7/(x – y) = 10
Solution:
Let’s substitute 1/(x + y) = u and 1/(x – y) = v, so the given equations becomes
5u – 2v = -1
15u + 7v = 10
For cross-multiplication, we use

Comparing the above two equations with the general form, we get

Hence, the solution for the given system of equations is x = 3 and y = 2.
10. 2/x + 3/y = 13
5/x – 4/y = -2
Solution:
Let 1/x = u and 1/y = v, so the equation becomes
2u + 3y = 13 ⇒ 2u + 3y – 13 = 0
5u – 4y = -2 ⇒ 5u – 4y + 2 = 0
For cross-multiplication, we use

Comparing the above two equations with the general form, we get

Hence, the solution for the given system of equations is x = 1/2 and y = 1/3.
11. 57/(x + y) + 6/(x – y) = 5
38/(x + y) + 21/(x – y) = 9
Solution:
Let’s substitute 1/(x + y) = u and 1/(x – y) = v, so the given equations becomes
57u + 6v = 5 ⇒ 57u + 6v – 5 = 0
38u + 21v = 9 ⇒ 38u + 21v – 9 = 0
For cross-multiplication, we use

Comparing the above two equations with the general form, we get

Hence, the solution for the given system of equations is x = 11 and y = 8.
12. xa – yb = 2
ax – by = a2-b2
Solution:
The given system of equations can be written as
xa – yb – 2 = 0
ax – by – (a2-b2) = 0
For cross-multiplication, we use

Comparing the above two equations with the general form, we get

Hence, the solution for the given system of equations is x = a and y = b.
13. x/a + y/b = a + b
x/a2 + y/b2 = 2
Solution:
The given system of equations can be written as
x/a + y/b – (a + b) = 0
x/a2 + y/b2 – 2 = 0
For cross-multiplication, we use

Comparing the above two equations with the general form, we get

Hence, the solution for the given system of equations is x = a2 and y = b2.
14. x/a = y/b
ax + by = a2 + b2
Solution:
The given system of equations can be written as
x/a – y/b = 0
ax + by – (a2 + b2) = 0
For cross-multiplication, we use

Comparing the above two equations with the general form, we get

Hence, the solution for the given system of equations is x = a and y = b.














Comments