The knowledge of the construction of graphs of linear equations in solving systems of simultaneous linear equations in two variables is practised in this exercise. The RD Sharma Solutions Class 10 can be a great help for students to clear their doubts and also help prepare them for exams. All the solutions are developed by experts at BYJU’S by matching students from all levels. The RD Sharma Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.2 PDF is given below for any reference related to the exercise problems.
RD Sharma Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.2
Access RD Sharma Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.2
Solve the following system of equations graphically:
1. x + y = 3
2x + 5y = 12
Solution:
Given,
x + y = 3……. (i)
2x + 5y = 12……. (ii)
For equation (i),
When y = 0, we have x =3
When x= 0, we have y =3
Thus we have the following table giving points on the line x + y = 3
| x | 0 | 3 |
| y | 3 | 0 |
For equation (ii),
We solve for y:
⇒ y = (12 – 2x)/5
So, when x = 1
y = (12 – 2(1))/5 = 2
And, when x = 6
⇒ y = (12 – 2(6))/5 = 0
Thus we have the following table giving points on the line 2x + 5y = 12
| x | 1 | 6 |
| y | 2 | 0 |
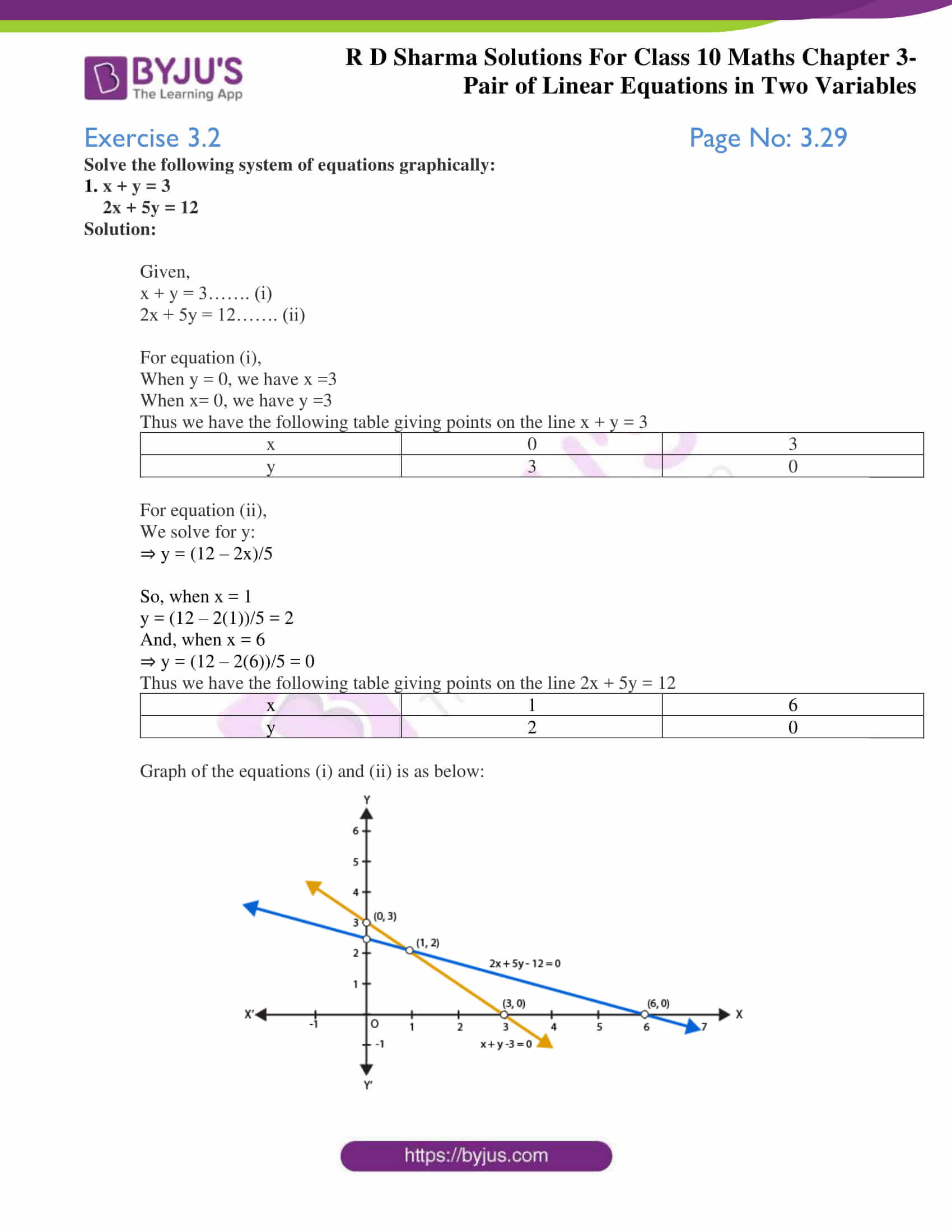
Graph of the equations (i) and (ii) is as below:

Clearly the two lines intersect at a single point P (1, 2)
Hence, x= 1 and y = 2
2. x – 2y = 5
2x + 3y = 10
Solution:
Given,
x – 2y = 5……. (i)
2x + 3y = 10……. (ii)
For equation (i),
⇒ y = (x – 5)/2
When y = 0, we have x = 5
When x = 1, we have y = -2
Thus we have the following table giving points on the line x – 2y = 5
| x | 5 | 1 |
| y | 0 | -2 |
For equation (ii),
We solve for y:
⇒ y = (10 – 2x)/3
So, when x = 5
y = (10 – 2(5))/3 = 0
And, when x = 2
⇒ y = (10 – 2(2))/3 =2
Thus, we have the following table giving points on the line 2x + 3y = 10
| x | 5 | 2 |
| y | 0 | 2 |
Graph of the equations (i) and (ii) is as below:

Clearly the two lines intersect at a single point P (5, 0)
Hence, x= 5 and y = 0
3. 3x+ y + 1 = 0
2x – 3y + 8 = 0
Solution:
Given,
3x+ y + 1 = 0 ……. (i)
2x – 3y + 8 = 0……. (ii)
For equation (i),
⇒ y = -(1 + 3x)
When x = 0, we have y = -1
When x = -1, we have y = 2
Thus, we have the following table giving points on the line 3x+ y + 1 = 0
| x | -1 | 0 |
| y | 2 | -1 |
For equation (ii),
We solve for y:
⇒ y = (2x + 8)/ 3
So, when x = -4
y = (2(-4) + 8)/3 = 0
And, when x = -1
⇒ y = (2(-1) + 8)/3 = 2
Thus we have the following table giving points on the line 2x – 3y + 8 = 0
| x | -4 | -1 |
| y | 0 | 2 |
Graph of the equations (i) and (ii) is as below:

Clearly the two lines intersect at a single point P (-1, 2)
Hence, x= -4 and y = 0
4. 2x + y – 3 = 0
2x – 3y – 7 = 0
Solution:
Given,
2x + y – 3 = 0……. (i)
2x – 3y – 7 = 0……. (ii)
For equation (i),
⇒ y = (3 – 2x)
When x = 0, we have y = (3 – 2(0)) = 3
When x = 1, we have y = (3 – 2(1)) = 1
Thus we have the following table giving points on the line 2x + y – 3 = 0
| x | 0 | 1 |
| y | 3 | 1 |
For equation (ii),
We solve for y:
⇒ y = (2x – 7)/ 3
So, when x = 2
y = (2(2) – 7)/3 = -1
And, when x = 5
⇒ y = (2(5) – 7)/3 = 1
Thus we have the following table giving points on the line 2x – 3y – 7 = 0
| x | 2 | 5 |
| y | -1 | 1 |
Graph of the equations (i) and (ii) is as below:

Clearly the two lines intersect at a single point P (2, -1)
Hence, x= 2 and y = -1
5. x + y = 6
x – y = 2
Solution:
Given,
x + y = 6……. (i)
x – y = 2……. (ii)
For equation (i),
⇒ y = (6 – x)
When x = 2, we have y = (6 – 2)) = 4
When x = 3, we have y = (6 – 3) = 3
Thus we have the following table giving points on the line x + y = 6
| x | 2 | 3 |
| y | 4 | 3 |
For equation (ii),
We solve for y:
⇒ y = (x – 2)
So, when x = 2
y = (0 – 2) = -2
And, when x = 5
⇒ y = (2 – 2) = 0
Thus we have the following table giving points on the line x – y = 2
| x | 0 | 2 |
| y | -2 | 0 |
Graph of the equations (i) and (ii) is as below:

Clearly the two lines intersect at a single point P (4, 2)
Hence, x= 4 and y = 2
6. x – 2y = 6
3x – 6y = 0
Solution:
Given,
x – 2y = 6……. (i)
3x – 6y = 0……. (ii)
For equation (i),
⇒ y = (x – 6)/2
When x = 2, we have y = (2 – 6)/2 = -2
When x = 0, we have y = (0 – 6)/2 = -3
Thus we have the following table giving points on the line x – 2y = 6
| x | 2 | 0 |
| y | -2 | -3 |
For equation (ii),
We solve for y:
⇒ y = x/ 2
So, when x = 0
y = 0/2 = 0
And, when x = 2
⇒ y = 2/2 = 1
Thus we have the following table giving points on the line 3x – 6y = 0
| x | 0 | 2 |
| y | 0 | 1 |
Graph of the equations (i) and (ii) is as below:

Clearly the two lines are parallel to each other. So, the two lines do not intersect.
Hence, the given system has no solutions.
7. x + y = 4
2x – 3y = 3
Solution:
Given,
x + y = 4……. (i)
2x – 3y = 3……. (ii)
For equation (i),
⇒ y = (4 – x)
When x = 4, we have y = (4 – 4) = 0
When x = 2, we have y = (4 – 2) = 2
Thus we have the following table giving points on the line x + y = 4
| x | 4 | 2 |
| y | 0 | 2 |
For equation (ii),
We solve for y:
⇒ y = (2x – 3)/3
So, when x = 3
y = (2(3) – 3)/3 = 1
And, when x = 0
⇒ y = (2(0) – 3)/3 = -1
Thus we have the following table giving points on the line 2x – 3y = 3
| x | 3 | 0 |
| y | 1 | -1 |
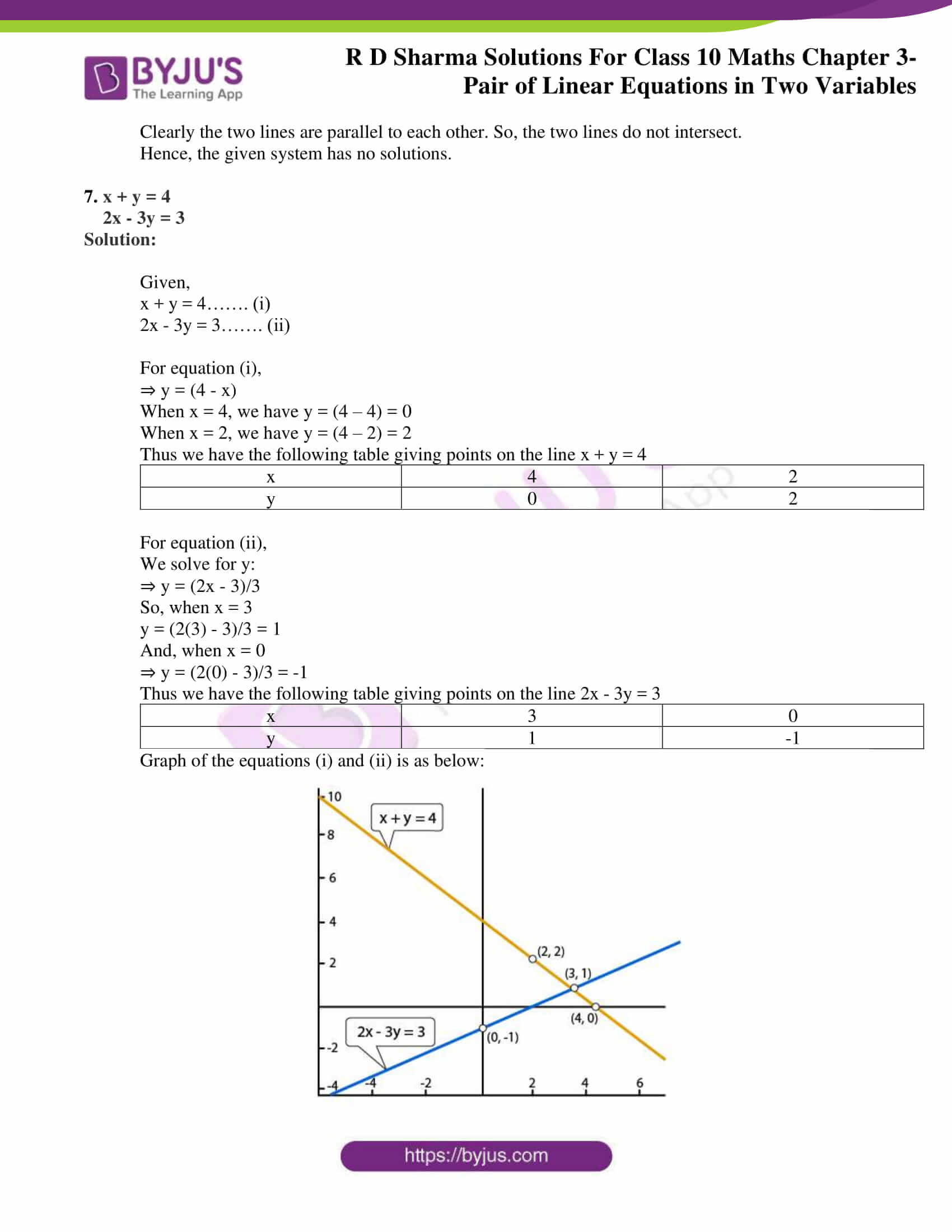
Graph of the equations (i) and (ii) is as below:

Clearly the two lines intersect at a single point P (3, 1)
Hence, x= 3 and y = 1
8. 2x + 3y = 4
x – y + 3 = 0
Solution:
Given,
2x + 3y = 4……. (i)
x – y + 3 = 0……. (ii)
For equation (i),
⇒ y = (4 – 2x) /3
When x = -1, we have y = (4 – 2(-1))/3 = 2
When x = 2, we have y = (4 – 2(2))/3 = 0
Thus we have the following table giving points on the line 2x + 3y = 4
| x | -1 | 2 |
| y | 2 | 0 |
For equation (ii),
We solve for y:
⇒ y = (x + 3)
So, when x = 0
y = ( 0 + 3) = 3
And, when x = 1
⇒ y = ( 1 + 3) = 4
Thus we have the following table giving points on the line x – y + 3 = 0
| x | 0 | 1 |
| y | 3 | 4 |
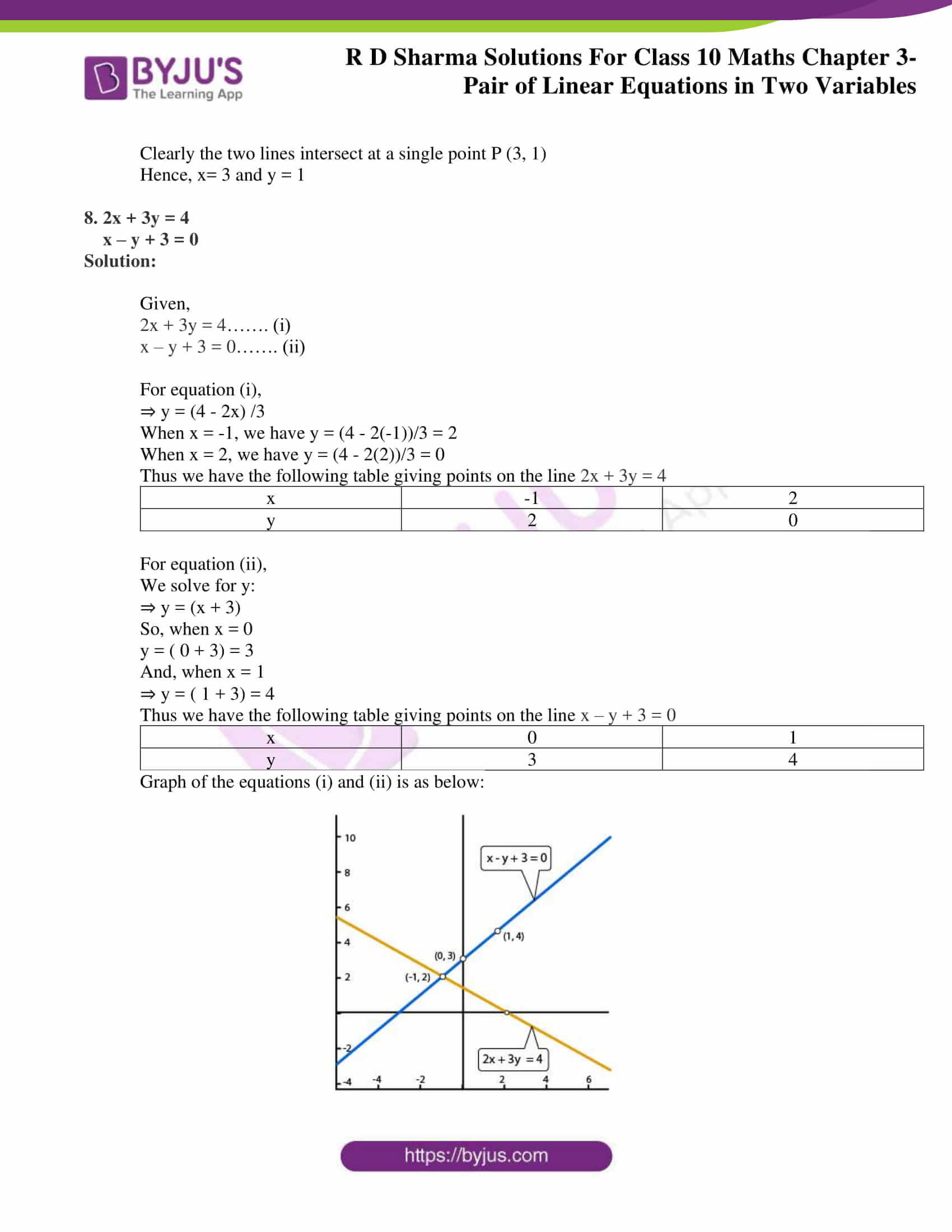
Graph of the equations (i) and (ii) is as below:

Clearly the two lines intersect at a single point P (-1, 2)
Hence, x= -1 and y = 2
9. 2x – 3y + 13 = 0
3x – 2y + 12 = 0
Solution:
Given,
2x – 3y + 13 = 0……. (i)
3x – 2y + 12 = 0……. (ii)
For equation (i),
⇒ y = (2x + 13) /3
When x = -5, we have y = (2(-5) + 13))/3 = 1
When x = -2, we have y = (2(-2) + 13))/3 = 3
Thus we have the following table giving points on the line 2x – 3y + 13 = 0
| x | -5 | -2 |
| y | 1 | 3 |
For equation (ii),
We solve for y:
⇒ y = (3x + 12)/2
So, when x = -4
y = (3(-4) + 12)/2 = 0
And, when x = -2
⇒ y = (3(-2) + 12)/2 = 3
Thus we have the following table giving points on the line 3x – 2y + 12 = 0
| x | -4 | -2 |
| y | 0 | 3 |
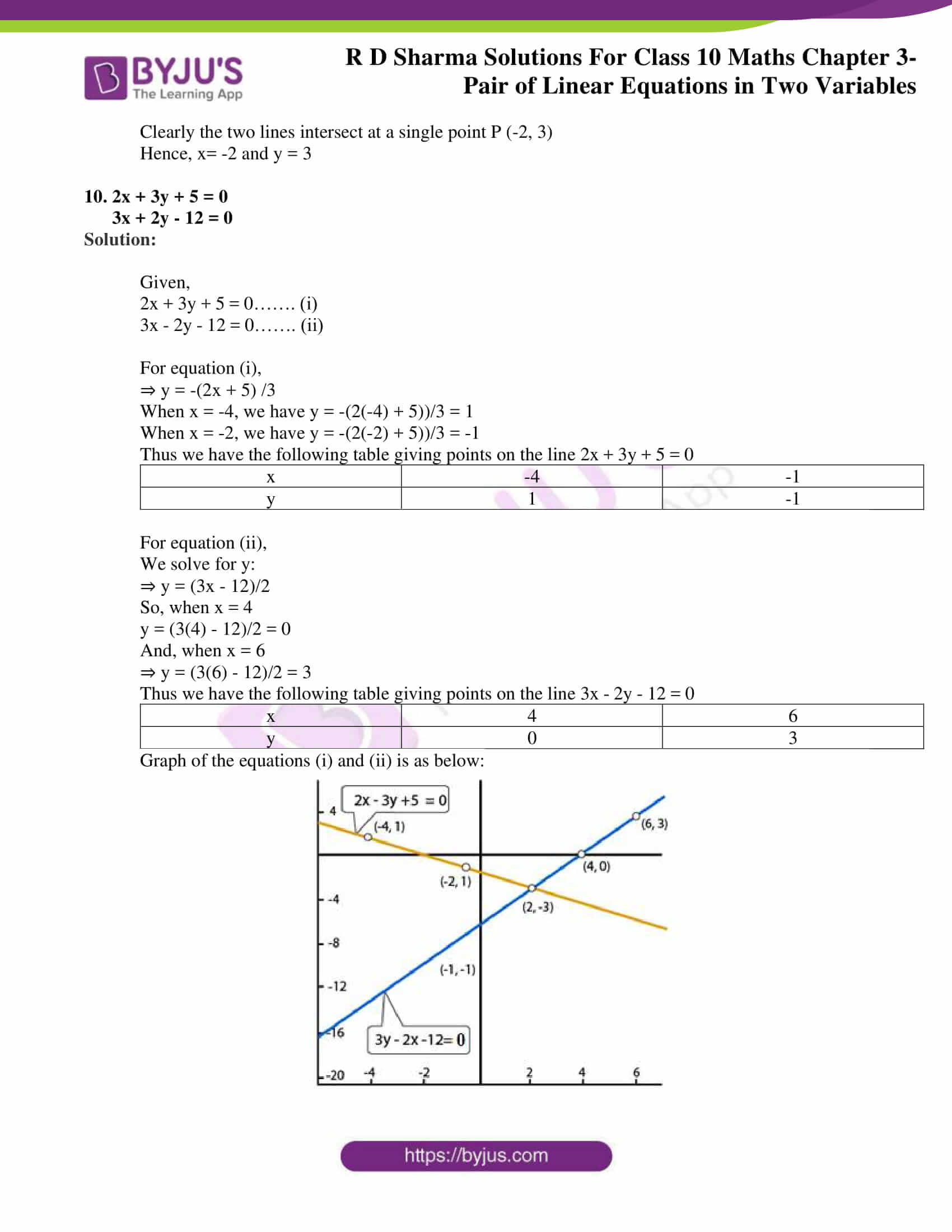
Graph of the equations (i) and (ii) is as below:

Clearly the two lines intersect at a single point P (-2, 3)
Hence, x= -2 and y = 3
10. 2x + 3y + 5 = 0
3x + 2y – 12 = 0
Solution:
Given,
2x + 3y + 5 = 0……. (i)
3x – 2y – 12 = 0……. (ii)
For equation (i),
⇒ y = -(2x + 5) /3
When x = -4, we have y = -(2(-4) + 5))/3 = 1
When x = -2, we have y = -(2(-2) + 5))/3 = -1
Thus we have the following table giving points on the line 2x + 3y + 5 = 0
| x | -4 | -1 |
| y | 1 | -1 |
For equation (ii),
We solve for y:
⇒ y = (3x – 12)/2
So, when x = 4
y = (3(4) – 12)/2 = 0
And, when x = 6
⇒ y = (3(6) – 12)/2 = 3
Thus we have the following table giving points on the line 3x – 2y – 12 = 0
| x | 4 | 6 |
| y | 0 | 3 |
Graph of the equations (i) and (ii) is as below:

Clearly the two lines intersect at a single point P (2, -3)
Hence, x= 2 and y = -3
Show graphically that each one of the following systems of equation has infinitely many solution:
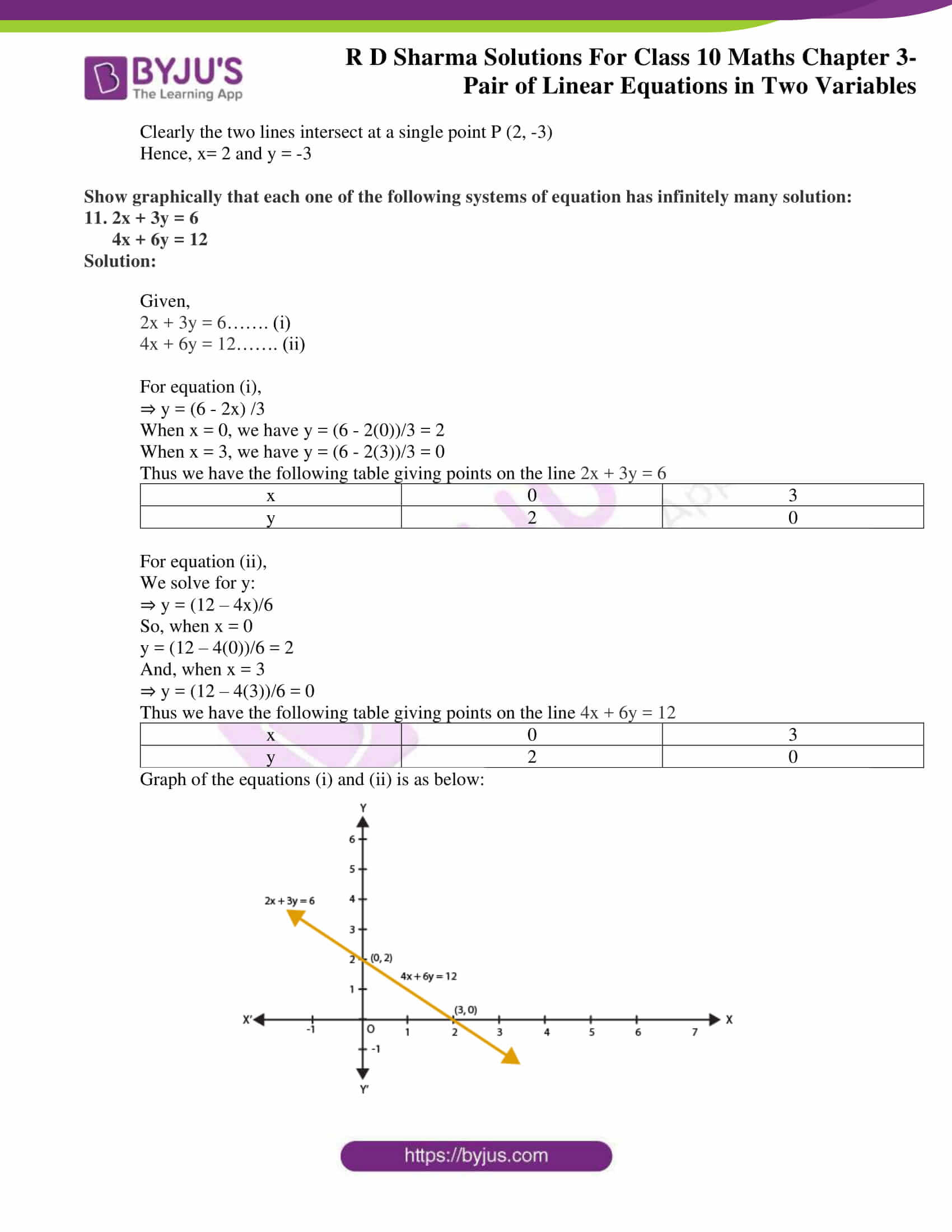
11. 2x + 3y = 6
4x + 6y = 12
Solution:
Given,
2x + 3y = 6……. (i)
4x + 6y = 12……. (ii)
For equation (i),
⇒ y = (6 – 2x) /3
When x = 0, we have y = (6 – 2(0))/3 = 2
When x = 3, we have y = (6 – 2(3))/3 = 0
Thus we have the following table giving points on the line 2x + 3y = 6
| x | 0 | 3 |
| y | 2 | 0 |
For equation (ii),
We solve for y:
⇒ y = (12 – 4x)/6
So, when x = 0
y = (12 – 4(0))/6 = 2
And, when x = 3
⇒ y = (12 – 4(3))/6 = 0
Thus we have the following table giving points on the line 4x + 6y = 12
| x | 0 | 3 |
| y | 2 | 0 |
Graph of the equations (i) and (ii) is as below:

Thus, the graphs of the two equations are coincident.
Hence, the system of equations has infinitely many solutions.
12. x – 2y = 5
3x – 6y = 15
Solution:
Given,
x – 2y = 5……. (i)
3x – 6y = 15……. (ii)
For equation (i),
⇒ y = (x – 5) /2
When x = 3, we have y = (3 – 5) /2 = -1
When x = 5, we have y = (5 – 5) /2 = 0
Thus we have the following table giving points on the line x – 2y = 5
| x | 3 | 5 |
| y | -1 | 0 |
For equation (ii),
We solve for y:
⇒ y = (3x – 15)/6
So, when x = 1
y = (3(1) – 15)/6= -2
And, when x = -1
⇒ y = (3(-1) – 15)/6= -3
Thus we have the following table giving points on the line 3x – 6y = 15
| x | 1 | -1 |
| y | -2 | -3 |
Graph of the equations (i) and (ii) is as below:

Thus, the graphs of the two equations are coincident.
Hence, the system of equations has infinitely many solutions.
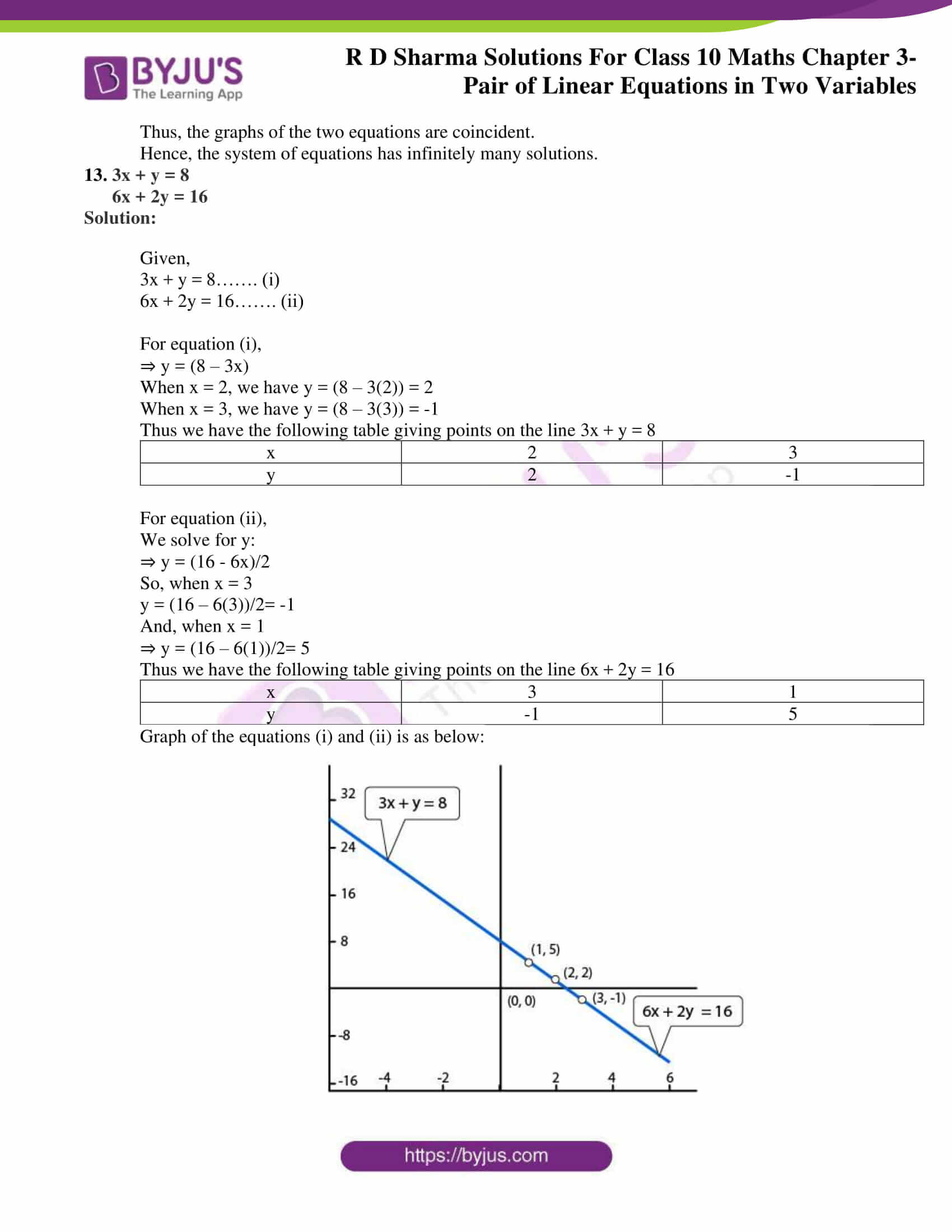
13. 3x + y = 8
6x + 2y = 16
Solution:
Given,
3x + y = 8……. (i)
6x + 2y = 16……. (ii)
For equation (i),
⇒ y = (8 – 3x)
When x = 2, we have y = (8 – 3(2)) = 2
When x = 3, we have y = (8 – 3(3)) = -1
Thus we have the following table giving points on the line 3x + y = 8
| x | 2 | 3 |
| y | 2 | -1 |
For equation (ii),
We solve for y:
⇒ y = (16 – 6x)/2
So, when x = 3
y = (16 – 6(3))/2= -1
And, when x = 1
⇒ y = (16 – 6(1))/2= 5
Thus we have the following table giving points on the line 6x + 2y = 16
| x | 3 | 1 |
| y | -1 | 5 |
Graph of the equations (i) and (ii) is as below:

Thus, the graphs of the two equations are coincident.
Hence, the system of equations has infinitely many solutions.
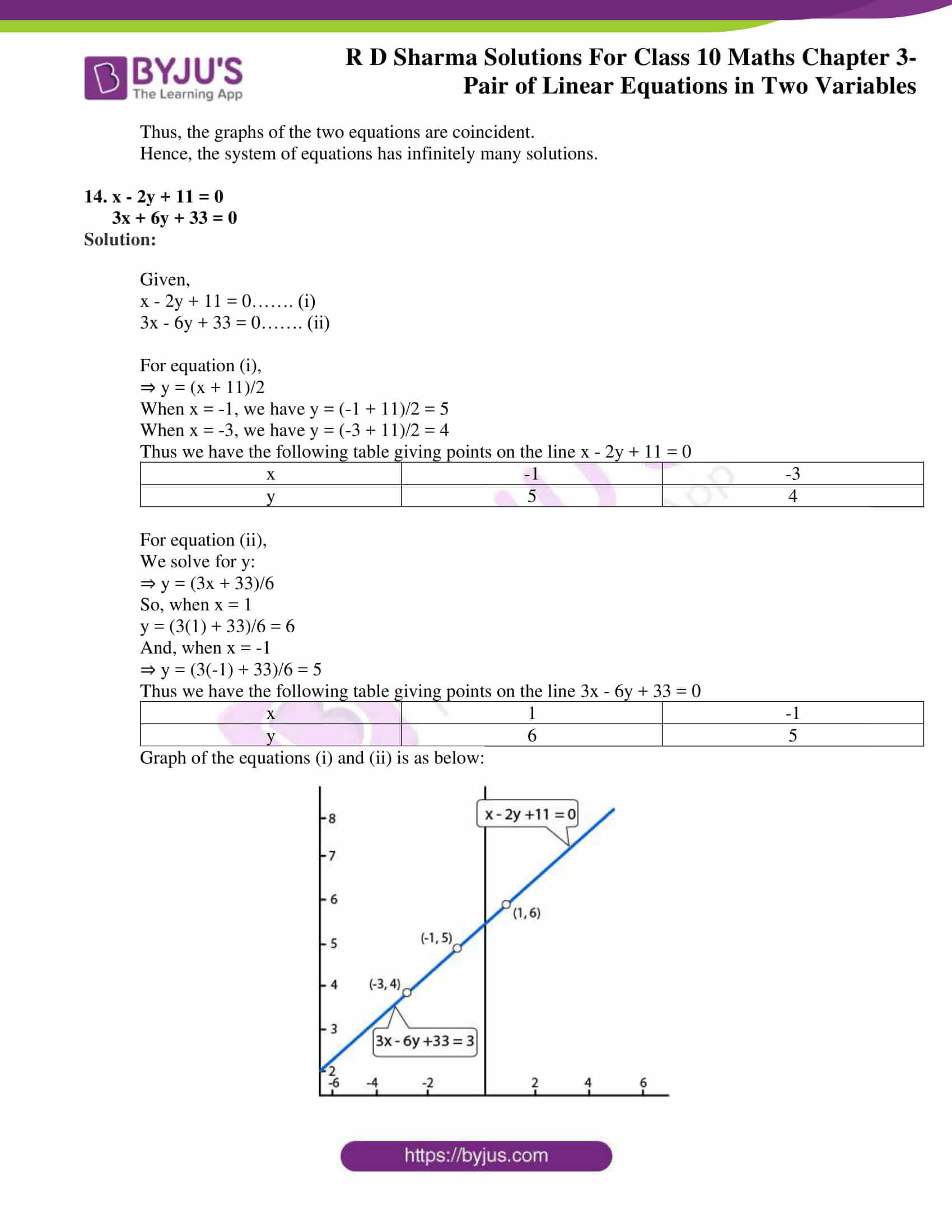
14. x – 2y + 11 = 0
3x + 6y + 33 = 0
Solution:
Given,
x – 2y + 11 = 0……. (i)
3x – 6y + 33 = 0……. (ii)
For equation (i),
⇒ y = (x + 11)/2
When x = -1, we have y = (-1 + 11)/2 = 5
When x = -3, we have y = (-3 + 11)/2 = 4
Thus we have the following table giving points on the line x – 2y + 11 = 0
| x | -1 | -3 |
| y | 5 | 4 |
For equation (ii),
We solve for y:
⇒ y = (3x + 33)/6
So, when x = 1
y = (3(1) + 33)/6 = 6
And, when x = -1
⇒ y = (3(-1) + 33)/6 = 5
Thus we have the following table giving points on the line 3x – 6y + 33 = 0
| x | 1 | -1 |
| y | 6 | 5 |
Graph of the equations (i) and (ii) is as below:

Thus, the graphs of the two equations are coincident.
Hence, the system of equations has infinitely many solutions.
Show graphically that each one of the following systems of equations is in-consistent (i.e has no solution):
15. 3x – 5y = 20
6x – 10y = – 40
Solution:
Given,
3x – 5y = 20……. (i)
6x – 10y = – 40……. (ii)
For equation (i),
⇒ y = (3x – 20)/5
When x = 5, we have y = (3(5) – 20)/5 = -1
When x = 0, we have y = (3(0) – 20)/5 = -4
Thus we have the following table giving points on the line 3x – 5y = 20
| x | 5 | 0 |
| y | -1 | -4 |
For equation (ii),
We solve for y:
⇒ y = (6x + 40)/10
So, when x = 0
y = (6(0) + 40)/10 = 4
And, when x = -5
⇒ y = (6(-5) + 40)/10 = 1
Thus we have the following table giving points on the line 6x – 10y = – 40
| x | 0 | -5 |
| y | 4 | 1 |
Graph of the equations (i) and (ii) is as below:

It is clearly seen that, there is no common point between these two lines.
Hence, the given systems of equations is in-consistent.
16. x – 2y = 6
3x – 6y = 0
Solution:
Given,
x – 2y = 6……. (i)
3x – 6y = 0……. (ii)
For equation (i),
⇒ y = (x – 6)/2
When x = 6, we have y = (6 – 6)/2 = 0
When x = 2 we have y = (2 – 6)/2 = -2
Thus we have the following table giving points on the line x – 2y = 6
| x | 6 | 2 |
| y | 0 | -2 |
For equation (ii),
We solve for y:
⇒ y = x/2
So, when x = 0
y = 0/2 = 0
And, when x = 2
⇒ y = 2/2 = 1
Thus we have the following table giving points on the line 3x – 6y = 0
| x | 0 | 2 |
| y | 0 | 1 |
Graph of the equations (i) and (ii) is as below:

It is clearly seen that, there is no common point between these two lines.
Hence, the given systems of equations is in-consistent.
17. 2y – x = 9
6y – 3x = 21
Solution:
Given,
2y – x = 9……. (i)
6y – 3x = 21……. (ii)
For equation (i),
⇒ y = (x + 9)/2
When x = -3, we have y = (-3 + 9)/2= 3
When x = -1, we have y = (-1 + 9)/2= 4
Thus we have the following table giving points on the line 2y – x = 9
| x | -3 | -1 |
| y | 3 | 4 |
For equation (ii),
We solve for y:
⇒ y = (21 + 3x)/6
So, when x = -3
y = (21 + 3(-3))/6 = 2
And, when x = -1
⇒ y = (21 + 3(-1))/6 = 3
Thus we have the following table giving points on the line 6y – 3x = 21
| x | -3 | -1 |
| y | 2 | 3 |
Graph of the equations (i) and (ii) is as below:

It is clearly seen that, there is no common point between these two lines.
Hence, the given systems of equations is in-consistent.
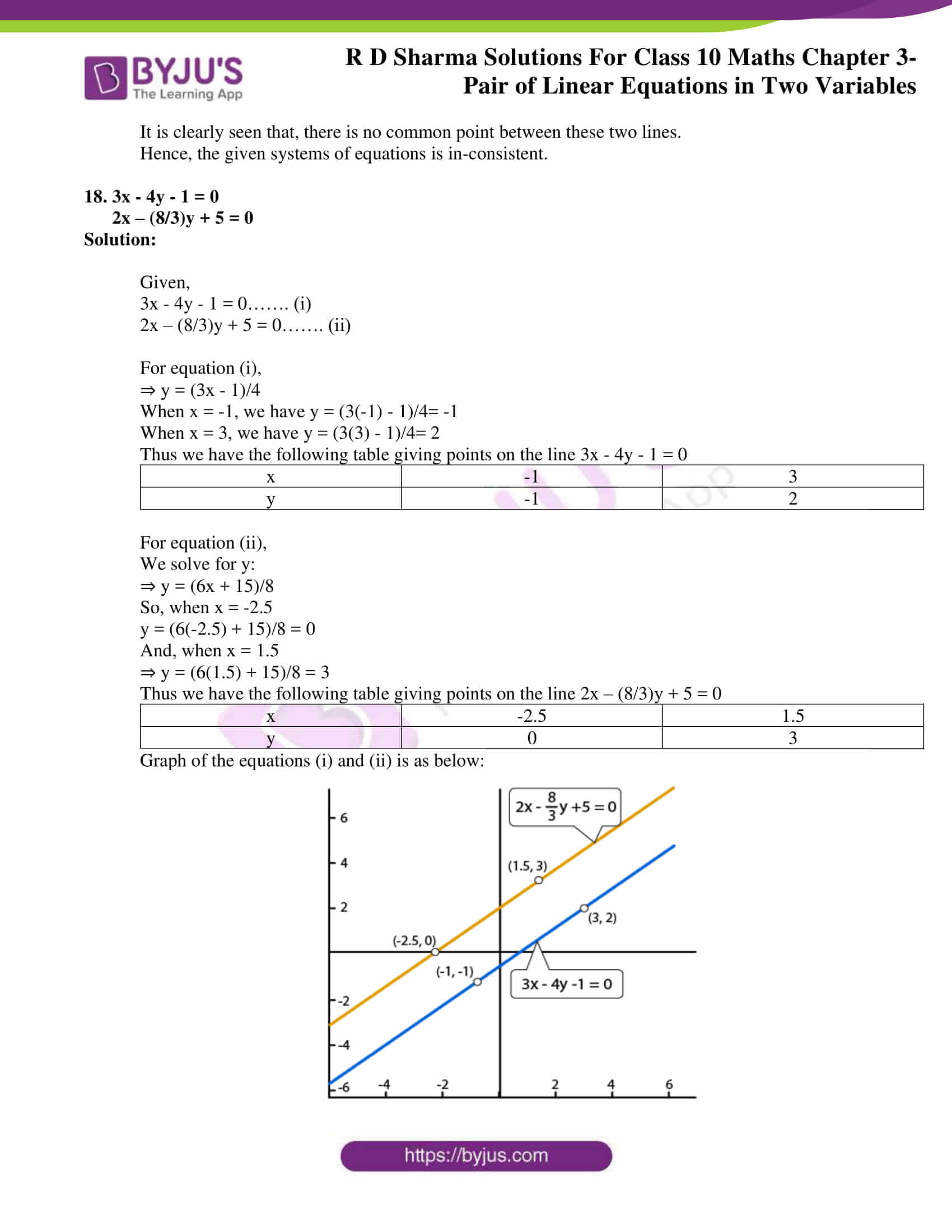
18. 3x – 4y – 1 = 0
2x – (8/3)y + 5 = 0
Solution:
Given,
3x – 4y – 1 = 0……. (i)
2x – (8/3)y + 5 = 0……. (ii)
For equation (i),
⇒ y = (3x – 1)/4
When x = -1, we have y = (3(-1) – 1)/4= -1
When x = 3, we have y = (3(3) – 1)/4= 2
Thus we have the following table giving points on the line 3x – 4y – 1 = 0
| x | -1 | 3 |
| y | -1 | 2 |
For equation (ii),
We solve for y:
⇒ y = (6x + 15)/8
So, when x = -2.5
y = (6(-2.5) + 15)/8 = 0
And, when x = 1.5
⇒ y = (6(1.5) + 15)/8 = 3
Thus we have the following table giving points on the line 2x – (8/3)y + 5 = 0
| x | -2.5 | 1.5 |
| y | 0 | 3 |
Graph of the equations (i) and (ii) is as below:

It is clearly seen that, there is no common point between these two lines.
Hence, the given systems of equations is in-consistent.
19. Determine graphically the vertices of the triangle, the equations of whose sides are given below:
(i) 2y – x = 8, 5y – x = 14 and y – 2x = 1
Solution:
Given,
2y – x = 8……. (i)
5y – x = 14……. (ii)
y – 2x = 1……… (iii)
For equation (i),
⇒ y = (x + 8)/2
When x = -4, we have y = (-4 + 8)/2 = 2
When x = 0, we have y = (0 + 8)/2 = 4
Thus we have the following table giving points on the line 2y – x = 8
| x | -4 | 0 |
| y | 2 | 4 |
For equation (ii),
We solve for y:
⇒ y = (x + 14)/5
So, when x = -4
y = ((-4) + 14)/5= 2
And, when x = 1
⇒ y = (1 + 14)/5= 3
Thus we have the following table giving points on the line 5y – x = 14
| x | -4 | 1 |
| y | 2 | 3 |
Finally, for equation (iii),
⇒ y = (2x + 1)
When x = -1, we have y = (2(-1) + 1) = -1
When x = 1, we have y = (2(1) + 1) = 3
Thus we have the following table giving points on the line y – 2x = 1
| x | -1 | 1 |
| y | 1 | 3 |
Graph of the equations (i), (ii) and (iii) is as below:

From the above graph, we observe that the lines taken in pairs intersect at points A(-4,2), B(1,3) and C(2,5)
Hence the vertices of the triangle are A(-4, 2), B(1, 3) and C(2,5)
(ii) y = x, y = 0 and 3x + 3y = 10
Solution:
Given,
y = x ……. (i)
y = 0 ……. (ii)
3x + 3y = 10……… (iii)
For equation (i),
When x = 1, we have y = 1
When x = -2, we have y = -2
Thus we have the following table giving points on the line y = x
| x | 1 | -2 |
| y | 1 | -2 |
For equation (ii),
When x = 0
y = 0
And, when x = 10/3
⇒ y = 0
Thus we have the following table giving points on the line y = 0
| x | 0 | 10/3 |
| y | 0 | 10/3 |
Finally, for equation (iii),
⇒ y = (10 – 3x)/3
When x = 1, we have y = (10 – 3(1))/3) = 7/3
When x = 2, we have y = (10 – 3(2))/3 = 4/3
Thus we have the following table giving points on the line 3x + 3y = 10
| x | 1 | 2 |
| y | 7/3 | 4/3 |
Graph of the equations (i), (ii) and (iii) is as below:

From the above graph, we observe that the lines taken in pairs intersect at points A(0,0) B(10/3,0) and C(5/3, 5/3)
Hence the vertices of the triangle are A(0,0) B(10/3,0) and C(5/3, 5/3).
20. Determine graphically whether the system of equations x – 2y = 2, 4x – 2y = 5 is consistent or in-consistent.
Solution:
Given,
x – 2y = 2……. (i)
4x – 2y = 5……. (ii)
For equation (i),
⇒ y = (x – 2)/2
When x = 2, we have y = (2 – 2)/2 = 0
When x = 0, we have y = (0 – 2)/2 = -1
Thus we have the following table giving points on the line x – 2y = 2
| x | 2 | 0 |
| y | 0 | -1 |
For equation (ii),
We solve for x:
⇒ x = (5 + 2y)/4
So, when y = 0
x = (5 + 2(0))/4 = 5/4
And, when y = 1.5
⇒ x = (5 + 2(1))/4 = 7/4
Thus we have the following table giving points on the line 4x – 2y = 5
| x | 5/4 | 7/4 |
| y | 0 | 1 |
Graph of the equations (i) and (ii) is as below:

It is clearly seen that the two lines intersect at (1,0)
Hence, the system of equations is consistent.
21. Determine by drawing graphs, whether the following system of linear equation has a unique solution or not:
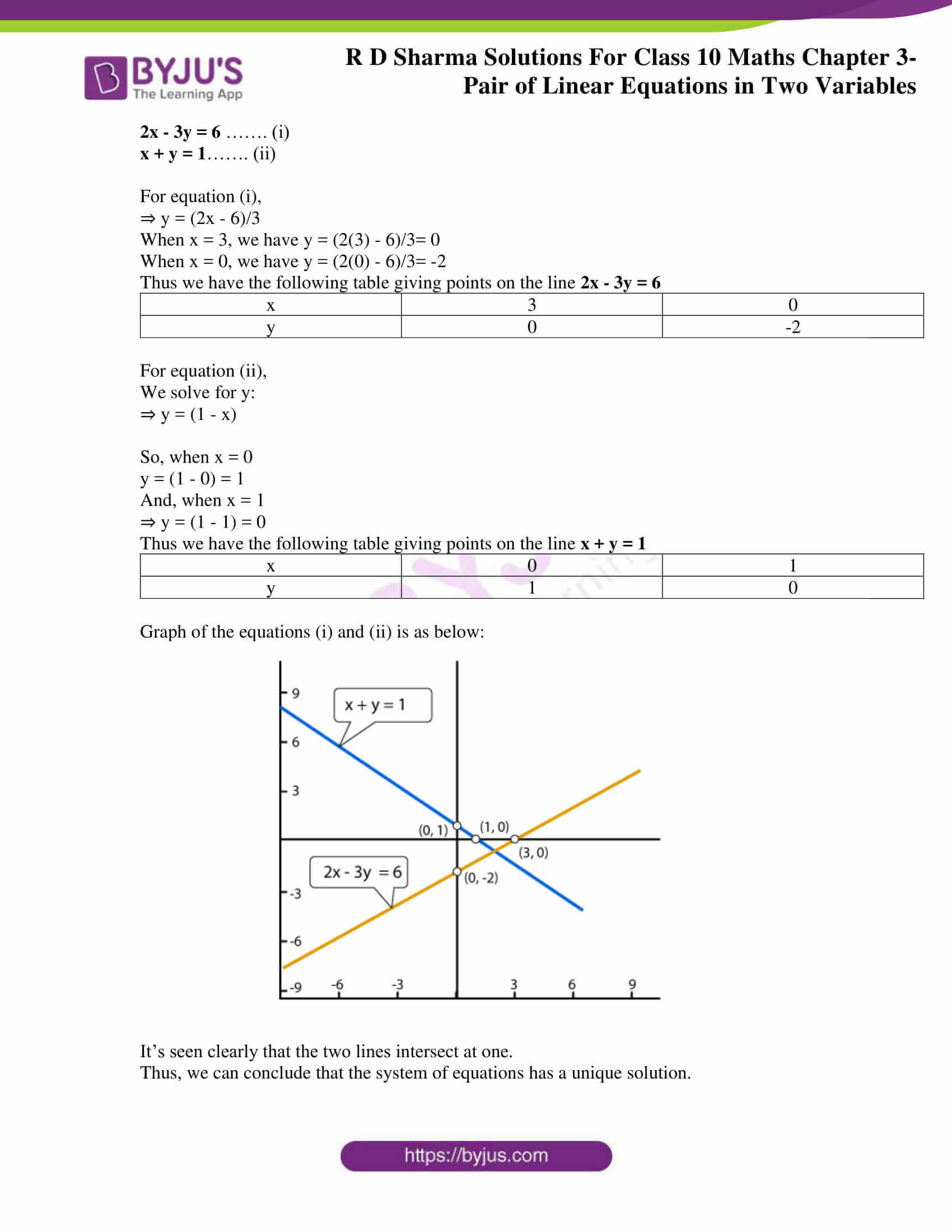
(i) 2x – 3y = 6 and x + y = 1
Solution:
Given,
2x – 3y = 6 ……. (i)
x + y = 1……. (ii)
For equation (i),
⇒ y = (2x – 6)/3
When x = 3, we have y = (2(3) – 6)/3= 0
When x = 0, we have y = (2(0) – 6)/3= -2
Thus we have the following table giving points on the line 2x – 3y = 6
| x | 3 | 0 |
| y | 0 | -2 |
For equation (ii),
We solve for y:
⇒ y = (1 – x)
So, when x = 0
y = (1 – 0) = 1
And, when x = 1
⇒ y = (1 – 1) = 0
Thus we have the following table giving points on the line x + y = 1
| x | 0 | 1 |
| y | 1 | 0 |
Graph of the equations (i) and (ii) is as below:

It’s seen clearly that the two lines intersect at one.
Thus, we can conclude that the system of equations has a unique solution.
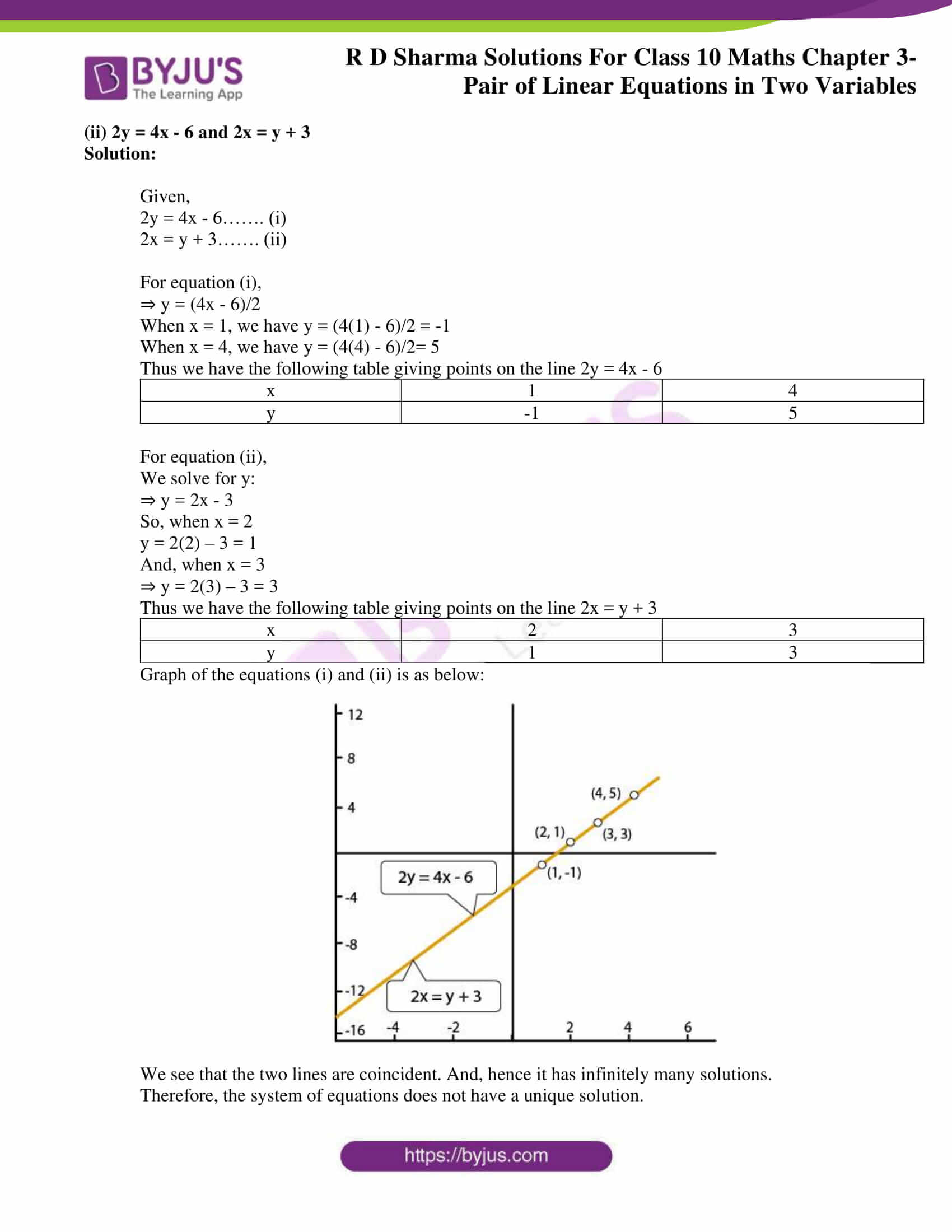
(ii) 2y = 4x – 6 and 2x = y + 3
Solution:
Given,
2y = 4x – 6……. (i)
2x = y + 3……. (ii)
For equation (i),
⇒ y = (4x – 6)/2
When x = 1, we have y = (4(1) – 6)/2 = -1
When x = 4, we have y = (4(4) – 6)/2= 5
Thus we have the following table giving points on the line 2y = 4x – 6
| x | 1 | 4 |
| y | -1 | 5 |
For equation (ii),
We solve for y:
⇒ y = 2x – 3
So, when x = 2
y = 2(2) – 3 = 1
And, when x = 3
⇒ y = 2(3) – 3 = 3
Thus we have the following table giving points on the line 2x = y + 3
| x | 2 | 3 |
| y | 1 | 3 |
Graph of the equations (i) and (ii) is as below:

We see that the two lines are coincident. And, hence it has infinitely many solutions.
Therefore, the system of equations does not have a unique solution.














Comments