Pearson Correlation Formula
The name correlation suggests the relationship between two variables as their Co-relation. The correlation coefficient is the measurement of correlation. To see how the two sets of data are connected, we make use of this formula. The linear dependency between the data set is done by the Pearson Correlation coefficient. It is also known as the Pearson product-moment correlation coefficient. The value of the Pearson correlation coefficient product is between -1 to +1. When the correlation coefficient comes down to zero, then the data is said to be not related. While, if we are getting the value of +1, then the data are positively correlated and -1 has a negative correlation.
The graphical representation of positive, negative and no correlation is shown below:
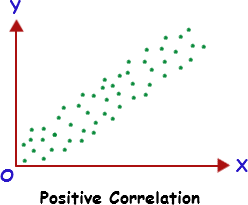
Positive Correlation


The Pearson correlation coefficient is denoted by the letter “r”. The formula for Pearson correlation coefficient r is given by:
\[\large r=\frac{n(\sum xy)-(\sum x)(\sum y)}{\sqrt{[n\sum x^{2}-(\sum x)^{2}][n\sum y^{2}-(\sum y)^{2}]}}\]
Where,
r = Pearson correlation coefficient
x = Values in the first set of data
y = Values in the second set of data
n = Total number of values.
Solved Example
Question: Marks obtained by 5 students in algebra and trigonometry as given below:
| Algebra | 15 | 16 | 12 | 10 | 8 |
| Trigonometry | 18 | 11 | 10 | 20 | 17 |
Calculate the Pearson correlation coefficient.
Solution:
Construct the following table:
| x | y | x2 | y2 | xy |
| 15 | 18 | 225 | 324 | 270 |
| 16 | 11 | 256 | 121 | 176 |
| 12 | 10 | 144 | 100 | 120 |
| 10 | 20 | 100 | 400 | 200 |
| 8 | 17 | 64 | 289 | 136 |
| \(\begin{array}{l}\sum x\end{array} \) = 61 |
\(\begin{array}{l}\sum y\end{array} \) = 76 |
\(\begin{array}{l}\sum x^{2}\end{array} \) = 789 |
\(\begin{array}{l}\sum y^{2}\end{array} \) = 1234 |
\(\begin{array}{l}\sum xy\end{array} \) = 902 |
Formula for Pearson correlation coefficient is given by:
r =
r =
r = -0.424
Comments