Cone is 3-D structure that is formed when we rotate the base of a right-angled triangle. Cone has a circular base and a vertex. The total surface area of a cone equals the area of the base plus the area of the curved surface. The area of the base, since has a circular shape, is equal to the area of the circle. The surface area of the cone is measured as per square units.

Sometimes the slant height will not be given in the question, so we need to find that out. The following example will show how to find the slant height.

The curved surface area of the cone is given by multiplying the base radius of the cone with pi and then multiplying the answer to the length of the side of the cone.

Now, the total surface area of the cone will be the area of the base plus the curved surface area of the cone.  

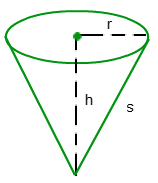
The formula for the Surface Area of Cone Formula is given as:

\[\large Curved\;Surface\;Area\;of\;cone=\pi rs\]

\[\large Total\;Surface\;Area\;of\;cone=\pi r \left (s+r \right )\]
Where,
r is the radius of cone.
h is the height of cone.
s is the slant height of the cone.

Solved Example

Question: Find the surface area of a cone of radius 7 cm and height 6 cm ?

Solution:

First, find out the Slant Height of the cone:

Formula to find Slant Height of the cone is 

Here,
r = 7
h = 6

So, 

Slant Height =

Now, find the curved surface area of the cone, using the formula.

CSA = πrs
= (22/7) ×7× 9.21
= 202.62 sq.cm