NCERT Solutions Class 5 Maths Chapter 3 - How Many Squares

NCERT Solutions Class 5 Maths Chapter 3 – How Many Squares, is provided here for students to prepare well for their exams. The NCERT Solutions are prepared by subject-matter experts according to the CBSE Syllabus (2023-2024).

NCERT Solutions for Class 5 Maths Chapter 3 – How Many Squares helps students to draw squares from a given set of dots. With questions related to measuring sides of squares, this chapter contains a series of questions which will help them improve their competence on the subject. Students can download NCERT Solutions for Class 5 Maths Chapter 3 in PDF in the link given below and start practising offline.

NCERT Solutions Class 5 Maths Chapter 3 – How Many Squares

Download PDF

carouselExampleControls112

Previous





Next

Access Solutions for NCERT Class 5 Maths Chapter 3 How Many Squares

Page: 34

1.

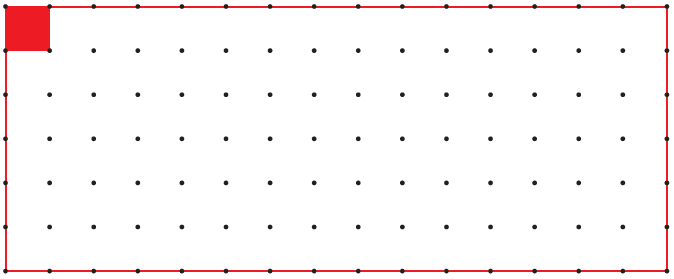
(i) Measure the side of the square on the dotted sheet. Draw here as many rectangles as possible using 12 such squares.

Solution:-

The side of the square on the dotted sheet is 1 cm.

(ii) How many rectangles could you make?

Solution:-

We can make 7 rectangles.

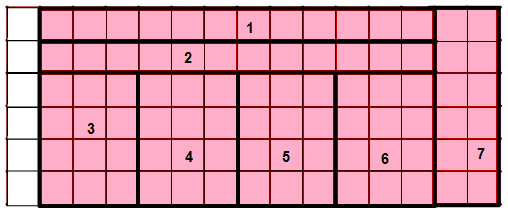
2. Each rectangle is made out of 12 equal squares, so all have the same area, but the length of the boundary will be different.

(i) Which of these rectangles has the longest perimeter?

Solution:-

From the above figure, we can say that rectangles 1 and 2 have the longest perimeter.

We know that, perimeter of rectangle = 2 (length + breadth)

= 2 (1 + 12)

= 2 × 13

= 26 cm

(ii) Which of these rectangles has the smallest perimeter?

Solution:-

From the above figure, we can say that rectangles 3, 4, 5 and 6 have the smallest perimeter.

We know that, perimeter of rectangle = 2 (length + breadth)

= 2 (3 + 5)

= 2 × 8

= 16 cm

3.

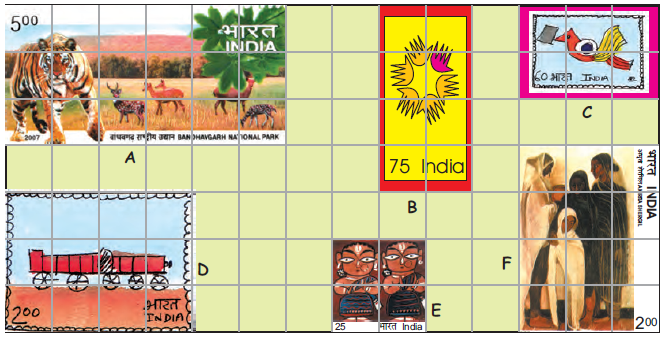
Look at these interesting stamps.

(a) How many squares of one-centimetre side do stamp A and stamp B cover? 

Solution:-

Stamp A covers 18 squares of the one-centimetre side, and Stamp B covers 8 squares of the one-centimetre side.

(b) Which stamp has the biggest area?

Solution:-

Stamp ‘A’ has the biggest area because it has 18 squares.

(i) How many squares of side 1 cm do this stamp cover?

Solution:-

This stamp has 18 squares of side 1 cm.

(ii) How much is the area of the biggest stamp?

Solution:-

The biggest stamp is in the shape of a rectangle.

Thus, the area of the biggest stamp is = length × breadth

= 3 × 6

= 18 cm²

c) Which two stamps have the same area?

Solution:-

Stamp ‘D’ and stamp ‘F’ have the same area.

(i) How much is the area of each of these stamps in square cm? 

Solution:-

We know that area of the rectangle = length × breadth

So, the area of the stamp ‘D’ = 3 × 4

= 12 cm²

Area of stamp ‘F’ = 4 × 3

= 12 cm²

Therefore, the area of stamp ‘D’ is equal to the area of stamp ‘F’.

d) The area of the smallest stamp is _____ square cm.

Solution:-

The area of smallest stamp ‘E’ = length × breadth

= 2 × 2

= 4 cm²

Therefore, the area of the smallest stamp is 4 square cm.

(i) The difference between the area of the smallest and the biggest stamp is _____ square cm.

Solution:-

Area of the biggest stamp = 18 cm²

Area of the smallest stamp = 4 cm²

Then,

The difference between the area of the smallest and the biggest stamp = 18 – 4

= 14 cm²

4. Guess

a) Which has the bigger area — one of your footprints or the page of the textbook?

Solution:-

When comparing the area of the footprints and the area of the page of the textbook, the area of the page of the textbook is bigger than the footprints.

b) Which has the smaller area – two five-rupee notes together or a hundred-rupee note?

Solution:-

A hundred rupee note has the smaller area.

c) Look at a 10 rupee note. Is its area more than hundred square cm?

Solution:-

No, the area of a 10 rupee note is not more than hundred square cm.

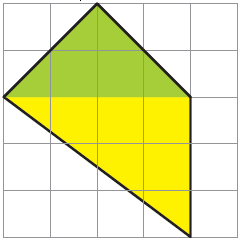
d) Is the area of the blue shape more than the area of the yellow shape? Why?

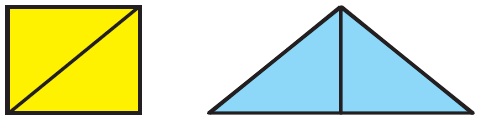
Solution:-

No, from the given image, we can say that the area of the blue shape is equal to the area of the yellow shape. Because the yellow and blue shaped figures are divided into two triangles of equal areas.

e) Is the perimeter of the yellow shape more than the perimeter of the blue shape? Why?

Solution:-

No, the perimeter of the yellow shape is less than the perimeter of the blue shape. With the help of a ruler, we can find that the length of the boundary of the blue shape is more than the length of the boundary of the yellow shape.

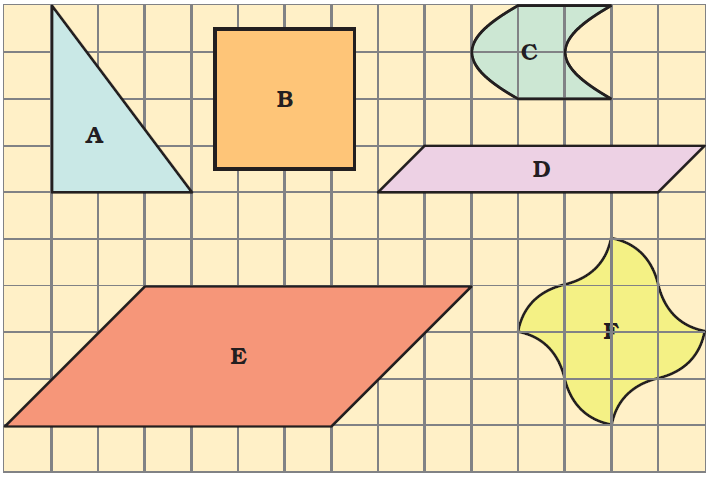
5. Write the area (in square cm) of the shapes below.

Solution:-

Area of triangle fig. A = ½ × base × height

= ½ × 3 × 4

= ½ × 12

= 6 cm²

Area of square fig. B = 4 complete square + 8 half squares + 4 quarter squares

= 4 + (½ × 8) + (¼ × 4)

= 4 + 4 + 1

= 9 cm²

Area of fig. C = 2 complete square + 4 half square

= 2 + (½ × 4)

= 2 + 2

= 4 cm²

Area of fig. D = 5 complete square + 2 half square

= 5 + (½ × 2)

= 5+ 1

= 6 cm²

Area of fig. E = 18 complete square + 6 half square

= 18 + (½ × 6)

= 18 + 3

= 21 cm²

Area of fig. F = 4 complete square + 4 more than half + 4 quarter square

= 4 + (¾ × 4) + (¼ × 4)

= 4 + 3 + 1

= 8 cm²

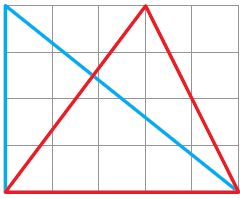
6. The blue triangle is half of the big rectangle. The area of the big rectangle is 20 square cm. So the area of the blue triangle is _______ square cm.

Solution:-

From the question,

The area of the big rectangle is 20 cm².

The area of the blue triangle is half of the big rectangle = 20/2

= 10 cm²

7. In the figure below, there are two halves of two different rectangles.

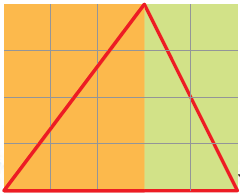
Find the area of the two rectangles in the figure. What is the area of the red triangle? Explain.

From the figure, we can say that,

The orange rectangle contains 12 squares

So, the area of the orange rectangle = 12 cm²

Then, the green rectangle contains 8 squares

So, the area of the green rectangle = 8 cm²

Now, the area of the orange portion of the triangle = 12/2 = 6 cm²

The area of the yellow portion of the triangle = 8/2 = 4 cm²

Therefore, the area of the red triangle = 6 + 4

= 10 cm²

8. Suruchi drew two sides of a shape. She asked Asif to complete the shape with two more sides so that its area was 10 square cm.

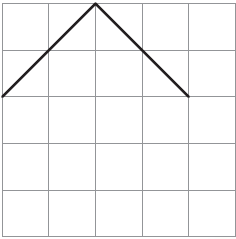
He completed the shape like the following:

(i) Is he correct? 

Solution:-

Yes, he is correct.

(ii) Explain how the green area is 4 square cm, and the yellow area is 6 square cm.

Solution:-

Green area = 2 complete square + 4 half square

= 2 + (½ × 4)

= 2 + 2

= 4 cm²

Yellow area = 3 complete square + 2 more than half + 2 half filled

= 3 + 2 + (½ × 2)

= 3 + 2 + 1

= 6 cm²

Practice Questions

1. This is one of the sides of a shape. Complete the shape so that its area is 4 square cm.

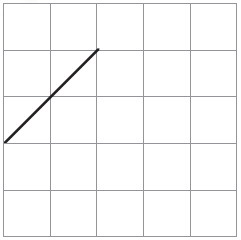
Solution:-

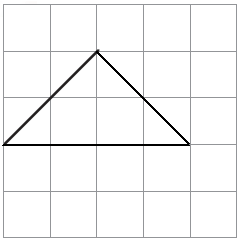
The completed shape = 2 complete square + 4 half square

= 2 + (½ × 4)

= 2 + 2

= 4 cm²

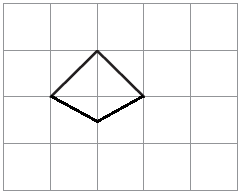
2. Two sides of a shape are drawn here. Complete the shape by drawing two more sides so that its area is less than 2 square cm.

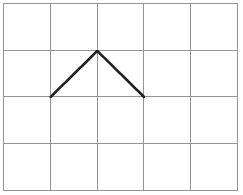
Solution:-

3. Here is a rectangle with an area of 20 square cm.

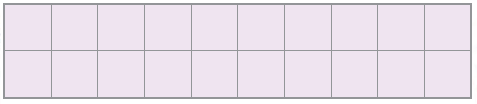
a) Draw one straight line in this rectangle to divide it into two equal triangles. What is the area of each of the triangles?

Solution:-

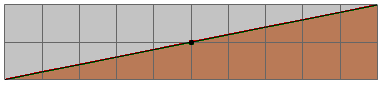
Area of rectangle = 10 × 2

= 20 cm²

Then, the area of two equal triangles = 20/2

= 10 cm²

Because it is given that a straight line divides the rectangle into two equal triangles.

b) Draw one straight line in this rectangle to divide it into two equal rectangles. What is the area of each of the smaller rectangles?

Solution:-

Area of big rectangle = 10 cm²

The area of each of the smaller rectangles = 20/2

= 10 cm²

c) Draw two straight lines in this rectangle to divide it into one rectangle and two equal triangles.

Solution:-

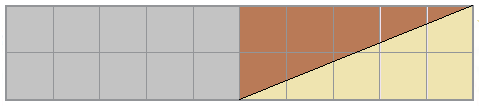
(i) What is the area of the rectangle?

Solution:-

Area of rectangle = length × breadth

= 2 × 5

= 10 cm²

(ii) What is the area of each of the triangles?

Solution:-

Area of each triangle = ½ × area of the smaller rectangle

= ½ × 10

= 5 cm²

4. Puzzle with five squares

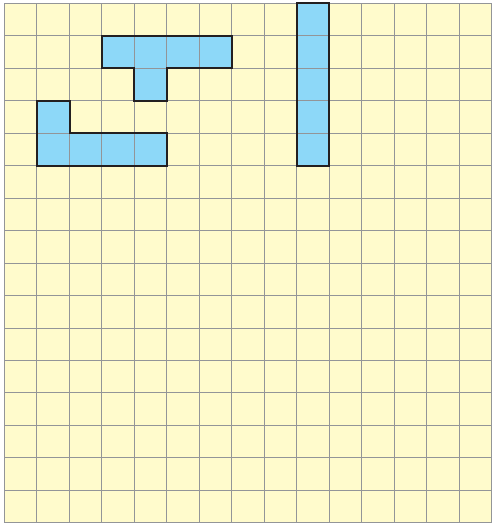
a) How many different shapes can you draw?

Solution:-

Using 5 squares, I can draw 12 shapes, as shown below:

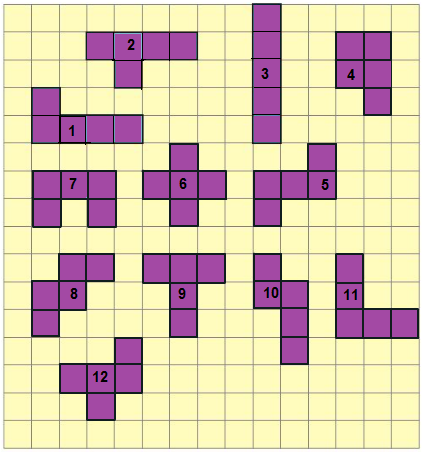
b) Which shape has the longest perimeter? How much?

Solution:-

Shape 4 has the smallest perimeter out of the 12 shapes; the rest of the shapes have the same perimeter, i.e. = 1 + 1 + 1 + 1 + 1 + 1+ 1 + 1 + 1 + 1 + 1 + 1 = 12 cm

c) Which shape has the shortest perimeter? How much?

Solution:-

Out of 12 shapes, 4 have the smallest perimeter.

i.e. = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 10 cm.

d) What is the area of the shapes (in square cm)?

Solution:-

There are 12 shapes, and each shape has five complete squares. The area of 1 square is equal to 1 cm².

So, the area of each shape = 1 × 5 = 5 cm²

5. Ziri tried to make some tiles. She started with a square of 2 cm side and made shapes like the following:

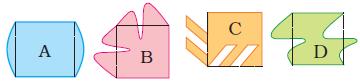
Look at them carefully and find out:

(i) Which of these shapes will tile a floor (without any gaps)? 

Solution:-

By observing the given figure, shape C and shape D will tile a floor without any gaps.