NCERT Solutions Class 10 Maths Chapter 1 Real Numbers Exercise 1.3 can be downloaded from here. These solutions for questions given in NCERT are prepared by our subject experts, thus a helpful resource for students appearing for Class 10 exams. These experts review this NCERT Maths Solution for Class 10 in two ways – chapter-wise and exercise-wise – so that they would be useful for students in solving problems easily.
They prefer to make these NCERT Solutions for Class 10 in such a way that they should be easily understandable by the students. Exercise 1.3 is the third exercise of Chapter- 1, Real Numbers in Class 10. The important topic discussed here is revisiting irrational numbers. It is important to have a basic understanding of rational and irrational numbers before solving Exercise 1.3. Students can also practise solving a problem by following the NCERT guidelines. The NCERT Class 10 solutions provided here follow the same.
Download the PDF of NCERT Solutions for Class 10 Maths Chapter 1 – Real Number Exercise 1.3
Access Answers to Maths NCERT Class 10 Chapter 1 – Real Number Exercise 1.3
1. Prove that √5 is irrational.
Solutions: Let us assume that √5 is a rational number.
i.e., √5 = x/y (where, x and y are co-primes)
y√5= x
Squaring both sides, we get
(y√5)2 = x2
⇒5y2 = x2……………………………….. (1)
Thus, x2 is divisible by 5, so x is also divisible by 5.
Let us say, x = 5k, for some value of k, and substituting the value of x in equation (1), we get
5y2 = (5k)2
⇒y2 = 5k2
is divisible by 5, it means y is divisible by 5.
Clearly, x and y are not co-primes. Thus, our assumption about √5 is rational is incorrect.
Hence, √5 is an irrational number.
2. Prove that 3 + 2√5 + is irrational.
Solutions: Let us assume 3 + 2√5 is rational.
Then, we can find co-prime x and y (y ≠ 0) such that 3 + 2√5 = x/y
Rearranging, we get
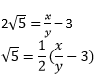
x and y are integers, thus
 is a rational number.
is a rational number.
Therefore, √5 is also a rational number. But this contradicts the fact that √5 is irrational.
So, we conclude that 3 + 2√5 is irrational.
3. Prove that the following are irrational.
(i) 1/√2
(ii) 7√5
(iii) 6 + √2
Solutions:
(i) 1/√2
Let us assume 1/√2 is rational.
Then, we can find co-prime x and y (y ≠ 0) such that 1/√2 = x/y
Rearranging, we get
√2 = y/x
x and y are integers; thus, √2 is a rational number, which contradicts the fact that √2 is irrational.
Hence, we can conclude that 1/√2 is irrational.
(ii) 7√5
Let us assume 7√5 is a rational number.
Then, we can find co-prime a and b (b ≠ 0) such that 7√5 = x/y
Rearranging, we get
√5 = x/7y
x and y are integers; thus, √5 is a rational number, which contradicts the fact that √5 is irrational.
Hence, we can conclude that 7√5 is irrational.
(iii) 6 +√2
Let us assume 6 +√2 is a rational number.
Then, we can find co-primes x and y (y ≠ 0) such that 6 +√2 = x/y
Rearranging, we get
√2 = (x/y) –
x and y are integers; thus, (x/y) – 6 is a rational number and therefore, √2 is rational. This contradicts the fact that √2 is an irrational number.
Hence, we can conclude that 6 +√2 is irrational.
Exercise 1.1 Solutions 5 Questions (4 long, 1 short)
Exercise 1.2 Solutions 14 Questions (4 long, 3 short)
Exercise 1.4 Solutions 3 Questions (3 short)
NCERT Solutions for Class 10 Maths Chapter 1 – Real Number Exercise 1.3
Exercise 1.3 of NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers is the third exercise of Chapter 1 of Class 10 Maths. Real Numbers is introduced in Class 9 and is discussed more in detail in Class 10. It is crucial to have a fair knowledge of the topic of irrational numbers to understand these solutions. The exercise discusses how to prove that root p is irrational.
- Revisiting Irrational Numbers – It includes 3 questions based on the theorem where question no. 3 has 3 roots to be proved as irrational.
Key Features of NCERT Solutions for Class 10 Maths Chapter 1 – Real Number Exercise 1.3
- These NCERT Solutions help students solve and revise all questions of Exercise 1.3.
- After going through the step-wise solutions given by our subject expert teachers, students will be able to score more marks.
- These solutions are prepared by following the NCERT Guidelines.
- The Solutions contain all the important questions from the examination point of view.



Comments