Redox reactions are oxidation-reduction chemical reactions in which the reactants undergo a change in their oxidation states. The term ‘redox’ is a short form of reduction-oxidation. All the redox reactions can be broken down into two different processes: a reduction process and an oxidation process.
Download Complete Chapter Notes of Redox Reactions
Download Now
The oxidation and reduction reactions always occur simultaneously in redox or oxidation-reduction reactions. The substance getting reduced in a chemical reaction is known as the oxidizing agent, while a substance that is getting oxidized is known as the reducing agent.
JEE Main 2021 LIVE Chemistry Paper Solutions 24 Feb Shift-1 Memory-based

Table of Contents
- Types
- Examples
- Oxidation and Reduction
- Oxidizing and Reducing Agents
- Identification of Oxidizing and Reducing Agents
- Balancing Redox Reaction
- Problems
- Applications
- FAQs
What Are Redox Reactions?
A redox reaction can be defined as a chemical reaction in which electrons are transferred between two reactants participating in it. This transfer of electrons can be identified by observing the changes in the oxidation states of the reacting species.
An illustration detailing the electron transfer between two reactants in a redox reaction is provided below.
In the illustration provided below, it can be observed that the reactant, an electron, was removed from reactant A, and this reactant is oxidized. Similarly, reactant B was handed an electron and was, therefore, reduced.
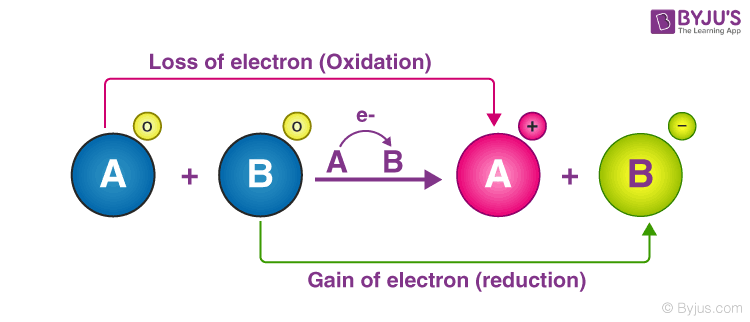
The loss of electrons and the corresponding increase in the oxidation state of a given reactant is called oxidation. The gain of electrons and the corresponding decrease in the oxidation state of a reactant is called reduction.
Electron-accepting species which tend to undergo a reduction in redox reactions are called oxidizing agents. An electron-donating species which tends to hand over electrons can be referred to as a reducing agent. These species tend to undergo oxidation. It can be noted that any redox reaction can be broken down into two half-reactions, namely, the oxidation half-reaction and the reduction half-reaction.
When writing these half-reactions separately, each of them must be balanced in a way that all the electrons are accounted for.
Types of Redox Reactions
The different types of redox reactions are
- Decomposition Reaction
- Combination Reaction
- Displacement Reaction
- Disproportionation Reactions
Decomposition Reaction
This kind of reaction involves the breakdown of a compound into different compounds. Examples of these types of reactions are
- 2NaH → 2Na + H2
- 2H2O → 2H2 + O2
- Na2CO3 → Na2O + CO2
All the above reactions result in the breakdown of smaller chemical compounds in the form of AB → A + B
But, there is a special case that confirms that all the decomposition reactions are not redox reactions.
For example, CaCO3 → CaO + CO2
Also Read: Types of Reactions
Combination Reaction
These reactions are the opposite of decomposition reactions and hence, involve the combination of two compounds to form a single compound in the form of A + B → AB. For example,
- H2 + Cl2 → 2HClC+O2→CO2
- 4Fe+ 3O2→2Fe2O3
Displacement Reaction
In this kind of reaction, an atom or an ion in a compound is replaced by an atom or an ion of another element. It can be represented in the form of X + YZ → XZ + Y. Further displacement reactions can be categorised into
- Metal displacement reaction
- Non-metal displacement reaction
Metal Displacement
In this type of reaction, a metal present in the compound is displaced by another metal. These types of reactions find their application in metallurgical processes where pure metals are obtained from their ores.
For example, CuSO4+Zn→Cu+ZnSO4
Non-metal Displacement
In this type of reaction, we can find a hydrogen displacement and, sometimes, rarely occurring reactions involving oxygen displacement.
Disproportionation Reactions
Disproportionation reactions are known as reactions in which a single reactant is oxidized and reduced.
For example, P4 + 3NaOH + 3H2O → 3NaH2PO2 + PH3
Disproportionation Reaction Video Lesson

Examples of Redox Reactions
A few examples of redox reactions, along with their oxidation and reduction half-reactions, are provided in this subsection.
Example 1: Reaction between Hydrogen and Fluorine
In the reaction between hydrogen and fluorine, the hydrogen is oxidized, whereas the fluorine is reduced. The reaction can be written as follows.
H2 + F2 → 2HF
The oxidation half-reaction is: H2 → 2H+ + 2e–
The reduction half-reaction is: F2 + 2e– → 2F–
The hydrogen and fluorine ions go on to combine in order to form hydrogen fluoride.
Example 2: Reaction between Zinc and Copper
This is a type of metal displacement reaction in which copper metal is obtained when zinc displaces the Cu2+ion in the copper sulphate solution, as shown in the reaction below.
Zn (s) + CuSO4 (aq) → ZnSO4 (aq) + Cu (s)
The oxidation half-reaction can be written as Zn → Zn2+ + 2e–
The reduction half-reaction can be written as Cu2+ + 2e– → Cu

Thus, copper is displaced from the copper sulphate solution by zinc in a redox reaction.
Example 3: Reaction between Iron and Hydrogen Peroxide
Fe2+ is oxidized to Fe3+ by hydrogen peroxide when an acid is present. This reaction is provided below.
2Fe2+ + H2O2 + 2H+ → 2Fe3+ + 2H2O
Oxidation half-reaction: Fe2+ → Fe3+ + e–
Reduction half-reaction: H2O2 + 2e– → 2 OH–
Thus, the hydroxide ion formed from the reduction of hydrogen peroxide combines with the proton donated by the acidic medium to form water.
Oxidation and Reduction Reaction
In order to understand redox reactions, let us first deal with oxidation and reduction reactions individually.
What Is the Oxidation Reaction?
Oxidation may be defined as the loss of electrons from a substance; the other definition of oxidation reactions states that the addition of oxygen or the more electronegative element or removal of hydrogen or the more electropositive element from a substance is called an oxidation reaction.
Following are some examples of oxidation reactions:
2S(s) + O2 (g) → SO2 (g) CH4 (g) + 2O2 (g) → CO2 (g) + 2H2O (l)
What Is Reduction Reaction?
Like oxidation reactions, reduction reactions are defined as the gain of electrons. Any substance that gains electrons during a chemical reaction gets reduced.
In other forms, the reduction reaction is stated as the addition of hydrogen or a more electropositive element or the removal of a more electronegative element or oxygen from a substance.
Below are some examples of reduction reactions:
- 2CH2CH2 (g) + H2 (g) → CH3CH3 (g)
- 2FeCl3 (aq) + H2 (g) → 2FeCl2 (aq) + 2HCl (aq)
Now, if we closely examine the above reaction, we would find that all the reactions above have both reduction and oxidation reactions.
The reaction in which FeCl3 is getting reduced as electronegative element chlorine is being removed from it. At the same time, hydrogen is getting oxidized due to the addition of chlorine, an electronegative element, in the same reaction.
Oxidizing and Reducing Agents
- The substance (atom, ion and molecule) that gains electrons and is thereby reduced to a low valency state is called an oxidising agent.
- The substance that loses electrons and is thereby oxidised to a higher valency state is called a reducing agent.
Important Oxidizing Agents
- Molecules are made up of electronegative elements. Eg: O2, O3, and X2 (halogens)
- Compounds containing an element that is in the higher oxidized state. Eg: KMnO4, K2Cv2O7, HNO3, KClo3
- Oxides of metals and non-metals. Eg: MgO, CuO, CrO3, P4O10
- Fluorine is the strongest oxidizing agent.
Important Reducing Agents
- All metals, for example, Na, Zn, Fe, Al
- A few non-metals, such as C, Hydrogen, S, P
- Hydracids, for example, HCl, HBr, HI, H2S
- A few compounds contain an element in the lower oxidation state. Examples include, FeCl2, FeSo4, SnCl2, Hg2Cl2
- Metallic hydrides, including NaH, LiH, CaH2, etc.
- Organic compounds like HCOOH
Lithium is the strongest reducing agent in the solution, and caesium is the strongest reducing agent in the absence of water. The substances which act as oxidizing as well as reducing agents are H2O2, SO2, H2SO3, HNO2 and NaNO2
Reduction Potential of a Half-reaction
Each half-reaction that makes up a redox reaction has a standard electrode potential. This potential equals the voltage produced by an electrochemical cell in which the cathode reaction is the half-reaction considered, whereas the anode is a standard hydrogen electrode.
This voltage produced by the half-reactions is called their reduction potentials (denoted by E0red). The value of the reduction potential of a half-reaction is positive for the oxidizing agents that are stronger than H+ and negative for the weaker ones.
Examples of the reduction potentials of some species are +2.866 V for F2 and -0.763 V for Zn2+.
Identification of Oxidizing and Reducing Agents
- If an element is in its higher possible oxidation state in a compound, it can function as an oxidising agent. Eg: KMnO4, K2Cr2O7, HNO3, H2SO4 and HClO4
- If an element is in its possible lower oxidation state in a compound, it can function as a reducing agent. Eg: H2S, H2C2O4, FeSO4 and SnCl2
- The compound will act as an oxidising agent if a highly electronegative element is in its highest oxidation state.
- The compound acts as a reducing agent if a highly electronegative element is in its lowest oxidation state.
Example: Identify the oxidizing agent and reducing agent in the reactions.
- \(\begin{array}{l}2N{{a}_{2}}{{S}_{2}}{{O}_{3}}+{{I}_{2}}\to N{{a}_{2}}{{S}_{4}}{{O}_{6}}+2NaI\end{array} \)
- \(\begin{array}{l}2FeC{{l}_{3}}+{{H}_{2}}S\to 2FeC{{l}_{2}}+S+2HCl\end{array} \)
- \(\begin{array}{l}3Mg+{{N}_{2}}\to M{{g}_{3}}{{N}_{2}}\end{array} \)
- \(\begin{array}{l}AgCN+C{{N}^{-}}\to {{\left[ Ag{{\left( CN \right)}_{2}} \right]}^{-}}\end{array} \)
Solution
| Oxidising agent
(Species reduced) |
Reducing agent
(Species oxidised) |
| I2 | Na2S2O3 |
| FeCl3 | H2S |
| N2 | None |
| None | None |
It is not a redox reaction. Each of the following reactions indicates the species oxidised, the species reduced, the oxidant and the reductant.
-
- Write the skeleton reaction to represent the chemical change.
- With the help of the oxidation number of elements, find out which element is undergoing oxidation/reduction.
- Add the electrons on the right for oxidation and the left for reduction.
- Multiply with a suitable integer such that the number of electrons taken and lost is the same.
Balancing Redox Reaction
There are two ways of balancing the redox reaction. One method is by using the change in oxidation number of oxidizing agent and the reducing agent, and the other method is based on dividing the redox reaction into two half reactions-one of reduction and another of oxidation.
Example 1: Write the balanced redox equation when ferrous sulphate is treated with acidified (H2SO4) Potassium Permanganate.
Step I
Step II

Thus, here Mn+7 is reduced to Mn+2
Balancing Redox Reaction by Oxidation State Method
This method is based on the fact that the number of electrons gained during the reduction reaction equals the number of electrons lost in oxidation.
Fe2+ is oxidised to Fe3+ oxidation:
Reduction:
Multiply the oxidation reaction by 5 and the reduction reaction by 2.

By substituting coefficient
⇒
Balancing Redox Reaction by Ion Electron Method (Half Reaction Method)
Steps:
-
- Divide the complete reaction into two half-reactions, one representing oxidation and the other representing reduction.
- First, balance other than ‘O’ and ‘H’ atoms.
- In an acidic or neutral medium, balance oxygen atoms by adding H2O molecules and balance H-atoms by adding H+ ions.
- In an alkaline medium, the oxygen atom is balanced by adding an H2O molecule, and an equal number of \(\begin{array}{l}O{{H}^{\Theta }}\end{array} \)ions are added on the opposite side, H+ atoms still unbalanced add OH–
- Balance the charges by the addition of electrons.
- Multiply with a suitable integer such that the number of electrons gets cancelled.
- Add both the half-reactions, similar terms are subtracted, and the final equation is written.
Problems on Balancing Redox Reactions
Example 1: Balance the following redox reaction in the acid medium by the ion-electron method.

| Reduction Half Reaction |
\(\begin{array}{l}MnO_{4}^{-}\to M{{n}^{+2}}\end{array} \) [Balance other than ‘O’ and H] |
\(\begin{array}{l}MnO_{4}^{-}\to M{{n}^{+2}}+4{{H}_{2}}O\end{array} \) [O atoms are balanced] |
\(\begin{array}{l}MnO_{4}^{-}+8{{H}^{+}}\to M{{n}^{+2}}+4{{H}_{2}}O\end{array} \) [H atoms are balanced] |
\(\begin{array}{l}MnO_{4}^{-}+8{{H}^{+}}+5{{e}^{-}}\to M{{n}^{+2}}+4{{H}_{2}}O\end{array} \) [Charges are balanced] |
\(\begin{array}{l}2\times [MnO_{4}^{-}+8{{H}^{+}}+5{{e}^{-}}\to M{{n}^{+2}}+4{{H}_{2}}O]\end{array} \) |
\(\begin{array}{l}[2MnO_{4}^{-}+16{{H}^{+}}+10{{e}^{-}}\to 2M{{n}^{+2}}+8{{H}_{2}}O]\end{array} \) |
| Oxidation Half Reaction |
\(\begin{array}{l}{{I}^{-}}\to {{I}_{2}}\end{array} \) \(\begin{array}{l}2{{I}^{-}}\to {{I}_{2}}\end{array} \) |
\(\begin{array}{l}2{{I}^{-}}\to {{I}_{2}}\end{array} \) |
\(\begin{array}{l}2{{I}^{-}}\to {{I}_{2}}\end{array} \) |
\(\begin{array}{l}2{{I}^{-}}\to {{I}_{2}}+2{{e}^{-}}\end{array} \) |
\(\begin{array}{l}5\times \left[2{{I}^{-}}\to {{I}_{2}}+2{{e}^{-}} \right]\end{array} \) |
\(\begin{array}{l}10{{I}^{-}}\to 5{{I}_{2}}+10{{e}^{-}}\end{array} \) |

Example 2: Balance the following redox reaction in an acid medium by ion-electron method.

Reduction Half Reaction
- \(\begin{array}{l}C{{r}_{2}}O_{7}^{-2}\to C{{r}^{+3}}\end{array} \)
- \(\begin{array}{l}C{{r}_{2}}O_{7}^{-2}\to 2C{{r}^{+3}}\end{array} \)
- \(\begin{array}{l}C{{r}_{2}}O_{7}^{-2}\to 2C{{r}^{+3}}+7{{H}_{2}}O\end{array} \)
- \(\begin{array}{l}C{{r}_{2}}O_{7}^{-2}+14{{H}^{+}}\to 2C{{r}^{+3}}+7{{H}_{2}}O\end{array} \)
- \(\begin{array}{l}C{{r}_{2}}O_{7}^{-2}+14{{H}^{+}}6{{e}^{-}}\to 2C{{r}^{+3}}+7{{H}_{2}}O\end{array} \)
Oxidation Half Reaction
- \(\begin{array}{l}SO_{3}^{-2}\to SO_{4}^{-2}\end{array} \)
- \(\begin{array}{l}SO_{3}^{-2}+{{H}_{2}}O\to SO_{4}^{-2}\end{array} \)
- \(\begin{array}{l}SO_{3}^{-2}+{{H}_{2}}O\to SO_{4}^{-2}+2H^{+}\end{array} \)
- \(\begin{array}{l}\left[ SO_{3}^{-2}+{{H}_{2}}O\to SO_{4}^{-2}+2{{H}^{+}}+2e \right]\times 3\end{array} \)
- \(\begin{array}{l}3SO_{3}^{-2}+3{{H}_{2}}O\to 3SO_{4}^{-2}+6{{H}^{+}}+6{{e}^{-}}\end{array} \)
- \(\begin{array}{l}\left[ C{{r}_{2}}O_{7}^{-2}+14{{H}^{+}}6{{e}^{-}}\to 2C{{r}^{+3}}+7{{H}_{2}}O \right]\end{array} \)
Example: 3 Balance the following reaction in the basic medium by ion-electron method.

Reduction Half Reaction
- \(\begin{array}{l}{{P}_{4}}\rightarrow{{}}P{{H}_{3}}\end{array} \)
- \(\begin{array}{l}{{P}_{4}}\rightarrow{{}}4P{{H}_{3}}\end{array} \)
- \(\begin{array}{l}{{P}_{4}}+12{{H}_{2}}O\rightarrow{{}}4P{{H}_{3}}+12O{{H}^{\Theta }}\end{array} \)
- \(\begin{array}{l}\left[ {{P}_{4}}+12{{H}_{2}}O+12{{e}^{-}}\rightarrow{{}}4P{{H}_{3}}+12O{{H}^{\Theta }} \right]\times 1\end{array} \)
Oxidation Half Reaction
- \(\begin{array}{l}{{P}_{4}}\rightarrow{{}}{{H}_{2}}PO_{2}^{-}\end{array} \)
- \(\begin{array}{l}{{P}_{4}}\rightarrow{{}}4{{H}_{2}}PO_{2}^{-}\end{array} \)
- \(\begin{array}{l}{{P}_{4}}+8{{H}_{2}}O\rightarrow{{}}4{{H}_{2}}PO_{2}^{-}+8O{{H}^{\Theta }}+8{{H}_{2}}O\end{array} \)
- \(\begin{array}{l}\left[ {{P}_{4}}+8{{H}_{2}}O+8O{{H}^{-}}\rightarrow{{}}4{{H}_{2}}PO_{2}^{-}+4{{e}^{-}}+8{{H}_{2}}O \right]\times 3\end{array} \)

Applications of Redox Reaction
Redox reactions have numerous industrial and everyday applications. A few of these applications are listed below.
Applications of Redox Reaction in Electrochemistry
The battery used for generating DC current uses a redox reaction to produce electrical energy.
Batteries or electrochemical cells used in our day-to-day life are also based on redox reactions. For example, storage cells are used in vehicles to supply all the electrical needs of the vehicles.
Redox Reaction in Combustion
Combustion is a type of oxidation-reduction reaction, and hence, it is a redox reaction. An explosion is a fast form of combustion; hence, the explosion can be treated as a redox reaction. Even the space shuttle uses redox reactions. The combination of ammonium perchlorate and powdered aluminium inside the rocket boosters gives rise to an oxidation-reduction reaction.
Applications in Photosynthesis
Green plants convert water and carbon dioxide into carbohydrates, defined as photosynthesis. The reaction is given as 6CO2 + 6H2O → C6H12O6 + 6O2

In the above reaction, we can see that carbon dioxide is reduced to carbohydrates while the water gets oxidized to oxygen; hence, it is a redox reaction. The energy is provided by the sunlight for this reaction. This reaction is a source of food for animals and plants.
Real-life Uses of Redox Reaction
- Production of some important chemicals is also based on electrolysis, which in turn, is based on redox reactions. Many chemicals, like caustic soda, chlorine, etc., are produced using redox reactions.
- Oxidation-reduction reactions also find their application in sanitising water and bleaching materials.
- The surfaces of many metals can be protected from corrosion by connecting them to sacrificial anodes, which undergo corrosion instead. A common example of this technique is the galvanisation of steel.
- The industrial production of cleaning products involves the oxidation process.
- Nitric acid, a component of many fertilisers, is produced from the oxidation reaction of ammonia.
- Electroplating is a process that uses redox reactions to apply a thin coating of a material on an object. Electroplating is used in the production of gold-plated jewellery.
- Many metals are separated from their ores with the help of redox reactions. One such example is the smelting of metal sulphides in the presence of reducing agents.
The main source of oxidation is oxygen, and therefore, redox reactions, or oxidation-reduction reactions, are responsible for food spoilage.
Redox Reactions – Top 10 Most Important and Expected JEE Questions

Balancing Redox Reactions for JEE Main & Advanced

Frequently Asked Questions on Redox Reactions
What are oxidation-reduction reactions?
What are oxidizing agents?
What are reducing agents?
How do you determine if a redox reaction has occurred?
1. Assign the oxidation numbers to all the atoms.
2. Compare the oxidation numbers from the reactant side to the product side.
3. In the case of a redox reaction, the oxidation numbers of two elements change from the reactant side to the product side.
- Element Oxidized: The one whose oxidation number is increased.
- Element Reduced: The one whose oxidation number is decreased.
Why is the reaction between hydrogen and fluorine a redox reaction?
Is every chemical reaction a redox reaction?
No, not every chemical reaction is a redox reaction. Reactions like double decompositions, acid-base neutralisation and precipitation reactions are non-redox reactions.
- Na2SO4 + BaCl2 = 2NaCl + BaSO4
- 2KI + Pb(NO3)2 = 2KNO3 + PbI2
- 2HCl + CaCO3 = H2O + CaCl2 + CO2
- HNO3 + NaOH = H2O + NaNO3
Some decomposition reactions are also non-redox reactions.
- NH4Cl = HCl + NH3
- CaCO3 = CO2 + CaO
- 2Al(OH)3 = 3H2O + Al2O3

Comments