RD Sharma Class 9 Mathematics Chapter 2 Exercise 2.2 Exponents of Real Numbers is provided here. This exercise is about rational exponents of real numbers and laws of rational exponents. RD Sharma Solutions Class 9 Chapter 2 are provided by subject experts at BYJU’S. Click on the link to download the free PDF of Chapter 2 Exercise 2.2.

RD Sharma Solutions for Class 9 Maths Chapter 2 Exponents of Real Numbers Exercise 2.2

Download PDF

carouselExampleControls111

Previous



Next

Access Answers to Maths RD Sharma Solutions for Class 9 Chapter 2 Exponents of Real Numbers Exercise 2.2 Page number 2.24

Question 1: Assuming that x, y, z are positive real numbers, simplify each of the following:

Solution:

Question 2: Simplify

Solution:

Question 3: Prove that

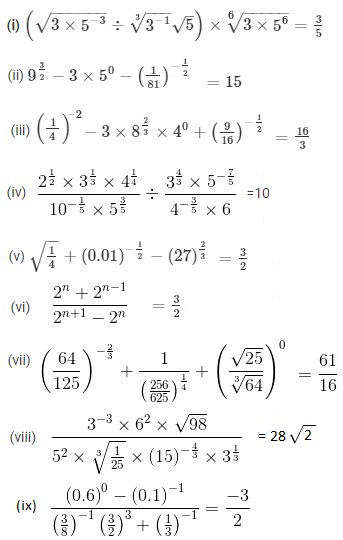
Solution:

(i) L.H.S.

=R.H.S.

Question 4.

Show that:

Solution:

RD Sharma Solutions for Class 9 Maths Chapter 2 Exponents of Real Numbers Exercise 2.2

RD Sharma Solutions Class 9 Maths Chapter 2 Exponents of Real Numbers Exercise 2.2 are based on the following topics:

• Rational exponents of real numbers
• nth root of a positive real number
• Rational powers
• Laws of rational exponents