RD Sharma Solutions for Class 9 Maths Chapter 2 Exponents of Real Numbers

RD Sharma Solutions Class 9 Maths Chapter 2 – Free PDF Download

RD Sharma Solutions for Class 9 Maths Chapter 2 – Exponents of Real Numbers help students to understand concepts like integral exponents of a real number, laws of exponents and rational powers. To facilitate easy learning and help students understand the concepts of exponents of Real Numbers, free RD Sharma Solutions are provided here, which can be further downloaded in the form of a PDF. Practising textbook questions following the RD Sharma Solutions for Class 9 Maths Chapter 2 improves conceptual knowledge among students. Those who aim to secure high marks are suggested to download solutions in PDF format from the link given below.

BYJU’S RD Sharma Solutions Class 9 Maths Chapter 2 provides a clear explanation of each concept in a simple and understandable language. These solutions have been designed keeping in mind the student’s grasping skills to solve the CBSE Class 9 Maths problems with ease. If a is a positive real number and n is a positive integer, then the principal n^th root of a is the unique positive real number x such that xⁿ = a. The principal n^th root of a is denoted by a^(1/n).

RD Sharma Solutions for Class 9 Maths Chapter 2 Exponents of Real Numbers

Download PDF

carouselExampleControls111

Previous



Next

Access Answers to Maths RD Sharma Solutions for Class 9 Chapter 2 Exponents of Real Numbers

Exercise 2.1

Question 1: Simplify the following

(i) 3(a⁴ b³)¹⁰ x 5 (a² b²)³

(ii) (2x ^-2 y³)³

Solution:

Using laws: (a^m)ⁿ = a^mn , a⁰ = 1, a^-m = 1/a and a^m x aⁿ = a^m+n]

(i) 3(a⁴ b³)¹⁰ x 5 (a² b²)³

On simplifying the given equation, we get;

= 3(a⁴⁰ b³⁰) x 5 (a⁶ b⁶)

= 15 (a⁴⁶ b³⁶)

(ii) (2x ^-2 y³)³

On simplifying the given equation, we get;

= (2³ x ^{-2 × 3} y^3×3)

= 8 x ^-6 y⁹

(iii)

Question 2: If a = 3 and b =-2, find the values of:

(i) a^a+ b^b

(ii) a^b + b^a

(iii) (a+b)^ab

Solution:

(i) a^a+ b^b

Now putting the values of ‘a’ and ‘b’, we get;

= 3³ + (−2)⁻²

= 3³ + (−1/2)²

= 27 + 1/4

= 109/4

(ii) a^b + b^a

Now putting the values of ‘a’ and ‘b’, we get;

= 3⁻² + (−2)³

= (1/3)² + (−2)³

= 1/9 – 8

= −71/9

(iii) (a+b)^ab

Now putting the values of ‘a’ and ‘b’, we get;

= (3 + (−2))³⁽⁻²⁾

= (3–2))⁻⁶

= 1⁻⁶

= 1

Question 3: Prove that

Solution:

(i) L.H.S. =

= R.H.S.

(ii) We have to prove here;

L.H.S. =

=R.H.S.

(iii) L.H.S. =

= R.H.S.

Question 4: Prove that

Solution:

(i) L.H.S

= R.H.S.

(ii) L.H.S

= R.H.S.

Question 5: Prove that

Solution:

(i) L.H.S.

= R.H.S.

(ii)

L.H.S.

= R.H.S.

Question 6: If abc = 1, show that

Solution:

Exercise 2.2

Question 1: Assuming that x, y, z are positive real numbers, simplify each of the following:

Solution:

Question 2: Simplify

Solution:

Question 3: Prove that

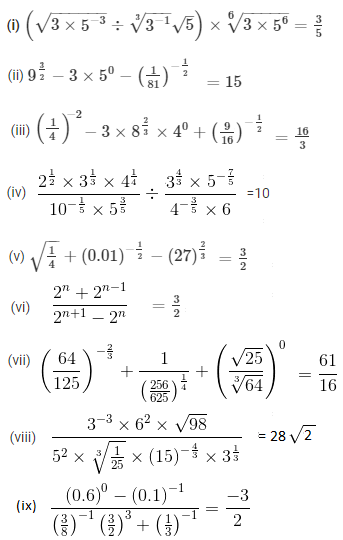
Solution:

(i) L.H.S.

=R.H.S.

Question 4.

Show that:

Solution:

Exercise-VSAQs

Question 1: Write (625)^–1/4 in decimal form.

Solution:

(625)^–1/4 = (5⁴)^-1/4 = 5^-1 = 1/5 = 0.2

Question 2: State the product law of exponents:

Solution:

To multiply two parts having same base, add the exponents.

Mathematically: x^m x xⁿ = x^{m +n}

Question 3: State the quotient law of exponents.

Solution:

To divide two exponents with the same base, subtract the powers.

Mathematically: x^m ÷ xⁿ = x^{m – n}

Question 4: State the power law of exponents.

Solution:

Power law of exponents :

(x^m)ⁿ = x^{m x n} = x^mn

Question 5: For any positive real number x, find the value of

Solution:

Question 6: Write the value of {5(8^1/3 + 27^1/3 ) ³}^1/4 .

Solution:

{5(8^1/3 + 27^1/3 ) ³}^1/4

= {5(2^3×1/3 + 3^3×1/3 ) ³}^1/4

= { 5(2 + 3)^3}^1/4

= (5⁴ ) ^1/4

= 5

RD Sharma Solutions for Class 9 Maths Chapter 2 Exponents of Real Numbers

In the 2nd chapter of Class 9 RD Sharma Solutions students will study important concepts on Exponents of Real Numbers, as listed below:

• Introduction to Exponents of Real Numbers
• Integral exponents of a Real Number
• Laws of Integral Exponents
• Rational Exponents of Real Number
• n^th root of a positive Real Number
• Laws of Rational Exponents

To know these concepts present in the RD Sharma textbook in detail, visit BYJU’S website. We also provide CBSE sample papers, previous year question papers and CBSE notes. This will help you in scoring well in your upcoming boards.