What is a Polygon?
A polygon is defined as a closed figure formed by line segments. These line segments intersect each other at their endpoints called vertices of the polygon. The line segments of a polygon are also known as edges or the sides of the polygon.
There are two types of a polygon, regular and irregular polygons. In regular polygons, all sides are congruent, but in irregular polygons, all the sides are not congruent. Some polygon are shown below:
Area of Polygon
- Area of a Triangle:
A triangle is a polygon with three sides. The area of a triangle is half of the product of the base and the height of the triangle.
Area of triangle, A = \(\frac{1}{2}\)bh
For example: Find the area of the triangle.
Solution :
A = \(\frac{1}{2}\)bh [Write the formula]
⇒ \(\frac{1}{2}\) x 6 x 8 [Substitute the values]
⇒ \(\frac{1}{2}\) x 48 [Multiply]
⇒ 24 [Divide]
So, the area of the given triangle is 24 square centimeters.
- Area of a Rectangle:
Rectangles are polygons with four sides and the opposite sides are congruent and parallel to each other. Each angle is a right angle at the intersection of the sides. The area of a rectangle is the product of the length and width of the rectangle.
Area of Rectangle, A = lb
For example: Find the area of the rectangle.
Solution :
The length is 15 in and width is 4 in.
A = l x b [Formula of area of rectangle]
A = 15 x 4 [Substitute 15 for l and 4 for b]
A = 60 [Multiply]
So, the area is 60 square inches.
- Area of a Square
Squares are polygons with four equal sides and each angle is 90°. All the sides of a square are also parallel to each other. The area of a square is the product of side length times side length.
Area of Square, A = s\(^2\)
For example: Find the area of the square.
Solution :
The length of the side of the square is 25 m.
A = s\(^2\) [Formula of area of square]
A = (25)\(^2\) [Substitute the values]
A = 625
So, the area of the square is 625 square meters.
- Area of a Parallelogram
A parallelogram is a polygon with four sides, and the opposite sides are congruent and parallel to each other. The area of a parallelogram is the product of its base and height.
Area of Parallelogram, A = bh
For Example : Find the area of the parallelogram.
Solution :
A = b x h [Write the formula]
A = 22 x 11 [Substitute the values]
A = 242 [Multiply]
So, the area of the parallelogram is 242 square yards.
- Area of a Trapezoid:
A trapezoid is a polygon with four sides, and just one pair of opposite sides are parallel to each other. The area of the trapezoid is half of the product of the height and the sum of the length of the parallel sides, called bases.
Area of a Trapezoid, A = \(\frac{1}{2}\)h (b\(_1\) + b\(_2\))
For Example: Find the area of the trapezoid.
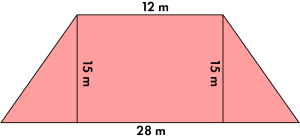
Solution :
A = \(\frac{1}{2}\)h (b\(_1\) + b\(_2\)) [Write the formula]
A = \(\frac{1}{2}\) (15) (28 + 12) [Substitute the values]
A = \(\frac{1}{2}\) (15)(40) [Add 28 and 12]
A = 300 [Simplify]
So, the area of the trapezoid is 300 square meters.
- Area of Kite:
Kites are polygons with four sides and both pairs of adjacent sides are equal in length. The area of a kite is the sum of the area of the two triangles formed by the diagonals of the kite.
Area of a kite: A = \(\frac{1}{2}\)h (b + a) + \(\frac{1}{2}\)H (b + a)
For Example : Find the area of the kite in the image.
Solution :
Divide the kite into two triangles and find the sum of the area of triangles.
A = \(\frac{1}{2}\)h (b + a) + \(\frac{1}{2}\)H (b + a) [Write the formula]
= \(\frac{1}{2}\)(24)(28) + \(\frac{1}{2}\)(15)(28) [Substitute the values]
= 336 + 210 [Simplify]
= 546 [Add]
So, the area of the kite is 546 square meters.
A polygon is a closed figure made by line segments.
The perimeter of a shape is the length of its boundary, and its area is the space enclosed by the boundary.
The area of the triangle is half of the product of its base and the height.
The area of the rectangle is the product of its length and width.
Square inches, square feet, square miles, square centimeters, square meters and square kilometers are some of the units used to represent the area of a figure.