Linear Equation
An equation with the highest exponent of 1 is said to be a linear equation. The graph of a linear equation is always a straight line.
We have to note that a linear equation in one variable is known as a one-variable linear equation.
The standard form of a one variable linear equation is \(Ax~+~B=0\), where x is the variable, A is the coefficient of \(x\), and \(B\) is the constant. Here, ‘\(A\)’ can not be zero.
For example: \(3x~+~8=0\)
A linear equation with two variables is a two-variable linear equation.
The standard form of a two variable linear equation is \(Ax~+~By~+~C=0\) where x and y are the variables, \(A\) is the coefficient of \(x,~B\) is the coefficient of, \(y\) and \(C\) is the constant.
For example: \(3x~-~2y~+~5=0\)
What is an Ordered pair?
An ordered pair is made up of the \(x\)(abscissa) and \(y\) (ordinate) coordinates, with two values written in a specific order within parentheses, \((x,~y)\), where x represents the distance from the origin along the \(x\)-axis, and \(y\) states the distance from the origin along the \(y\)-axis.
Graphing Linear Equations
The graph of a two-variable linear equation is a straight line. The graph of a linear equation can be drawn with the help of any two points \((x_1,~y_1)\) and \((x_2,~y_2)\). The following steps are to be followed to draw the graph:
Step 1: Make a table of values by putting values of \(x\) and getting the values of \(y\).
Step 2: Plot all the ordered pairs on the coordinate plane.
Step 3: Draw a line passing through all the ordered pairs.
For example: Plot a graph for \(3x~-~4y=12\).
Here, \(3x~-~4y=12\)
Graphing a Horizontal Line
The standard form of a horizontal line is \(y~=~b\) and the line passes through the point \((0,~b)\). The horizontal line is parallel to the \(x\)–axis.
Graphing a Vertical Line
The standard form of a vertical line is \(x=a\) and the line passes through the point \((a,~0)\). The vertical line is parallel to the \(y\)–axis.
Solved Examples
Example 1: Graph \(y=3x~-~2\).
Solution:
Step 1: Make a table of values.
x | \(y=3x~-~2\) | y | \((x,~y)\) |
|---|---|---|---|
-1 | \(y=3(- 1)~-~2\) | -5 | (-1, -5) |
0 | \(y=3(0)~-~2\) | -2 | (0, -2) |
1 | \(y=3(1)~-~2\) | 1 | (1, 1) |
2 | \(y=3(2)~-~2\) | 4 | (2, 4) |
Step 2: Plot the ordered pairs.
Step 3: Draw the line through the points.
Example 2: Graph \(y=5\)
Solution:
The graph of \(y=5\) is a horizontal line passing through (0, 5). Draw a horizontal line that passes through this point.
Example 3: Graph \(x=-~2\).
Solution:
The graph of\(x=-~2\) is a vertical line passing through (-2, 0). Draw a vertical line that passes through this point.
Example 4: The amount \(y\) (in dollars) of money in Sam’s saving accounts after \(x\) months is represented by the equation \(y=5x~+~200\). Draw the graph for the equation. In how many months Sam will have $300 as a savings in his account?
Solution:
Step 1: Make a table of values.
x | \(y=5x~+~200\) | y | \((x,~y)\) |
|---|---|---|---|
1 | \(y=5(1)~+~200\) | 205 | (1, 205) |
2 | \(y=5(2)~+~200\) | 210 | (2, 210) |
3 | \(y=5(3)~+~200\) | 215 | (3, 215) |
4 | \(y=5(4)~+~200\) | 220 | (4, 220) |
Step 2: Plot the ordered pairs.
Step 3: Draw the line through the points.
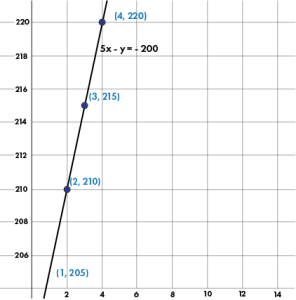
The total amount in the savings account is $300. The number of months in which the account has been saved by solving the equation after putting \(y=300\) .
\(y=5x~+~200\) Writing Equation
\(300=5x~+~200\) Substitute
\(x=20\) Simplify
Sam will take 20 months to save $300.
A linear equation is one in which the highest exponent of a variable is 1. Worksheets allow your child to see their processes and determine where they might be making conceptual or computational mistakes.
The equation whose highest exponent is greater than 1 is known as a non-linear equation.
A linear equation is represented by a straight line on a graph.
A solution is a value or a set of values when substituted for the unknown that makes the equation true.