RD Sharma Solutions for Class 9 Maths Chapter 4 Exercise 4.4 are available here. This exercise is about the sum and difference of cubes. We have covered various examples to illustrate the use of these identities to simplify the products of algebraic expressions. RD Sharma Class 9 Solutions cover important concepts that are more likely to be asked in the final examination. Students can download RD Sharma Class 9 Maths Chapter 4 Exercise 4.4 PDF from the below link.
RD Sharma Solutions for Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.4
Access Answers to Maths RD Sharma Solutions for Class 9 Chapter 4 Algebraic Identities Exercise 4.4 Page Number 4.23
Exercise 4.4 Page No: 4.23
Question 1: Find the following products:
(i) (3x + 2y)(9x2 – 6xy + 4y2)
(ii) (4x – 5y)(16x2 + 20xy + 25y2)
(iii) (7p4 + q)(49p8 – 7p4q + q2)
(iv) (x/2 + 2y)(x2/4 – xy + 4y2)
(v) (3/x – 5/y)(9/x2 + 25/y2 + 15/xy)
(vi) (3 + 5/x)(9 – 15/x + 25/x2)
(vii) (2/x + 3x)(4/x2 + 9x2 – 6)
(viii) (3/x – 2x2)(9/x2 + 4x4 – 6x)
(ix) (1 – x)(1 + x + x2)
(x) (1 + x)(1 – x + x2)
(xi) (x2 – 1)(x4 + x2 +1)
(xii) (x3 + 1)(x6 – x3 + 1)
Solution:
(i) (3x + 2y)(9x2 – 6xy + 4y2)
= (3x + 2y)[(3x)2 – (3x)(2y) + (2y)2)]
We know, a3 + b3 = (a + b)(a2 + b2 – ab)
= (3x)3 + (2y) 3
= 27x3 + 8y3
(ii) (4x – 5y)(16x2 + 20xy + 25y2)
= (4x – 5y)[(4x)2 + (4x)(5y) + (5y)2)]
We know, a3 – b3 = (a – b)(a2 + b2 + ab)
= (4x)3 – (5y) 3
= 64x3 – 125y3
(iii) (7p4 + q)(49p8 – 7p4q + q2)
= (7p4 + q)[(7p4)2 – (7p4)(q) + (q)2)]
We know, a3 + b3 = (a + b)(a2 + b2 – ab)
= (7p4)3 + (q) 3
= 343 p12 + q3
(iv) (x/2 + 2y)(x2/4 – xy + 4y2)
We know, a3 – b3 = (a – b)(a2 + b2 + ab)
(x/2 + 2y)(x2/4 – xy + 4y2)

(v) (3/x – 5/y)(9/x2 + 25/y2 + 15/xy)

(vi) (3 + 5/x)(9 – 15/x + 25/x2)

(vii) (2/x + 3x)(4/x2 + 9x2 – 6)

(viii) (3/x – 2x2)(9/x2 + 4x4 – 6x)

(ix) (1 – x)(1 + x + x2)
And we know, a3 – b3 = (a – b)(a2 + b2 + ab)
(1 – x)(1 + x + x2) can be written as
(1 – x)[(12 + (1)(x)+ x2)]
= (1)3 – (x)3
= 1 – x3
(x) (1 + x)(1 – x + x2)
And we know, a3 + b3 = (a + b)(a2 + b2 – ab)]
(1 + x)(1 – x + x2) can be written as,
(1 + x)[(12 – (1)(x) + x2)]
= (1)3 + (x) 3
= 1 + x3
(xi) (x2 – 1)(x4 + x2 +1) can be written as,
(x2 – 1)[(x2)2 – 12 + (x2)(1)]
= (x2)3 – 13
= x6 – 1
[using a3 – b3 = (a – b)(a2 + b2 + ab) ](xii) (x3 + 1)(x6 – x3 + 1) can be written as,
(x3 + 1)[(x3)2 – (x3)(1) + 12]
= (x3) 3 + 13
= x9 + 1
[using a3 + b3 = (a + b)(a2 + b2 – ab) ]Question 2: If x = 3 and y = -1, find the values of each of the following using in identity:
(i) (9y2 – 4x2)(81y4 + 36x2y2 + 16x4)
(ii) (3/x – x/3)(x2 /9 + 9/x2 + 1)
(iii) (x/7 + y/3)(x2/49 + y2/9 – xy/21)
(iv) (x/4 – y/3)(x2/16 + xy/12 + y2/9)
(v) (5/x + 5x)(25/x2 – 25 + 25x2)
Solution:
(i) (9y2 – 4x2)(81y4 + 36x2y2 + 16x4)
= (9y2 – 4x2) [(9y2 ) 2 + 9y2 x 4x2 + (4x2) 2 ]
= (9y2 ) 3 – (4x2)3
= 729 y6 – 64 x6
Put x = 3 and y = -1
= 729 – 46656
= – 45927
(ii) Put x = 3 and y = -1
(3/x – x/3)(x2 /9 + 9/x2 + 1)

(iii) Put x = 3 and y = -1
(x/7 + y/3)(x2/49 + y2/9 – xy/21)

(iv) Put x = 3 and y = -1
(x/4 – y/3)(x2/16 + xy/12 + y2/9)

(v) Put x = 3 and y = -1
(5/x + 5x)(25/x2 – 25 + 25x2)
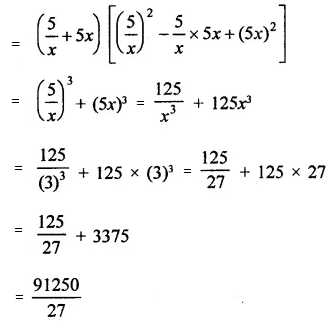
Question 3: If a + b = 10 and ab = 16, find the value of a2 – ab + b2 and a2 + ab + b2.
Solution:
a + b = 10, ab = 16
Squaring, a + b = 10, both sides
(a + b)2 = (10)2
a2 + b2 + 2ab = 100
a2 + b2 + 2 x 16 = 100
a2 + b2 + 32 = 100
a2 + b2 = 100 – 32 = 68
a2 + b2 = 68
Again, a2 – ab + b2 = a2 + b2 – ab = 68 – 16 = 52 and
a2 + ab + b2 = a2 + b2 + ab = 68 + 16 = 84
Question 4: If a + b = 8 and ab = 6, find the value of a3 + b3.
Solution:
a + b = 8, ab = 6
Cubing, a + b = 8, both sides, we get
(a + b)3 = (8)3
a3 + b3 + 3ab(a + b) = 512
a3 + b3 + 3 x 6 x 8 = 512
a3 + b3 + 144 = 512
a3 + b3 = 512 – 144 = 368
a3 + b3 = 368
RD Sharma Solutions for Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.4
RD Sharma Solutions for Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.4 are based on the sum and difference of cubes.
Important formulas:
- a3 + b3 = (a + b)3 – 3ab(a + b)
- or a3 + b3 = (a + b)(a2 – ab + b2)
- a3 – b3 = (a – b)3 – 3ab(a – b)
- or a3 – b3 = (a – b)(a2 + ab + b2)







Comments