RD Sharma Solutions for Class 9 Mathematics Chapter 4 Exercise 4.1 Algebraic Identities are provided here. The subject experts at BYJU’S have prepared RD Sharma Class 9 Maths Chapter 4 solutions in accordance with the latest CBSE syllabus for Class 9. Studying this chapter will help you to gain complete knowledge of algebraic identities. Students can download RD Sharma Exercise 4.1 by clicking on the link below.
RD Sharma Solutions for Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.1
Access Answers to RD Sharma Solutions for Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.1 Page Number 4.6
Exercise 4.1 Page No: 4.6
Question 1: Evaluate each of the following using identities:
(i) (2x – 1/x)2
(ii) (2x + y) (2x – y)
(iii) (a2b – b2a)2
(iv) (a – 0.1) (a + 0.1)
(v) (1.5.x2 – 0.3y2) (1.5x2 + 0.3y2)
Solution:
(i) (2x – 1/x)2
[Use identity: (a – b)2 = a2 + b2 – 2ab ](2x – 1/x)2 = (2x)2 + (1/x)2 – 2 (2x)(1/x)
= 4x2 + 1/x2 – 4
(ii) (2x + y) (2x – y)
[Use identity: (a – b)(a + b) = a2 – b2 ](2x + y) (2x – y) = (2x )2 – (y)2
= 4x2 – y2
(iii) (a2b – b2a)2
[Use identity: (a – b)2 = a2 + b2 – 2ab ]
(a2b – b2a)2 = (a2b) 2 + (b2a)2 – 2 (a2b)( b2a)
= a4b 2 + b4a2 – 2 a3b3
(iv) (a – 0.1) (a + 0.1)
[Use identity: (a – b)(a + b) = a2 – b2 ](a – 0.1) (a + 0.1) = (a)2 – (0.1)2
= (a)2 – 0.01
(v) (1.5 x2 – 0.3y2) (1.5 x2 + 0.3y2)
[Use identity: (a – b)(a + b) = a2 – b2 ](1.5 x2 – 0.3y2) (1.5x2 + 0.3y2) = (1.5 x2 ) 2 – (0.3y2)2
= 2.25 x4 – 0.09y4
Question 2: Evaluate each of the following using identities:
(i)(399)2
(ii)(0.98)2
(iii)991 x 1009
(iv) 117 x 83
Solution:
(i)

(ii)

(iii)

(iv)

Question 3: Simplify each of the following:
(i) 175 x 175 +2 x 175 x 25 + 25 x 25
(ii) 322 x 322 – 2 x 322 x 22 + 22 x 22
(iii) 0.76 x 0.76 + 2 x 0.76 x 0.24 + 0.24 x 0.24
(iv)

Solution:
(i) 175 x 175 +2 x 175 x 25 + 25 x 25 = (175)2 + 2 (175) (25) + (25)2
= (175 + 25)2
[Because a2+ b2+2ab = (a+b)2 ]= (200)2
= 40000
So, 175 x 175 +2 x 175 x 25 + 25 x 25 = 40000.
(ii) 322 x 322 – 2 x 322 x 22 + 22 x 22
= (322)2 – 2 x 322 x 22 + (22)2
= (322 – 22)2
[Because a2+ b2-2ab = (a-b)2]= (300)2
= 90000
So, 322 x 322 – 2 x 322 x 22 + 22 x 22= 90000.
(iii) 0.76 x 0.76 + 2 x 0.76 x 0.24 + 0.24 x 0.24
= (0.76) 2 + 2 x 0.76 x 0.24 + (0.24) 2
= (0.76+0.24) 2
[ Because a2+ b2+2ab = (a+b)2]= (1.00)2
= 1
So, 0.76 x 0.76 + 2 x 0.76 x 0.24 + 0.24 x 0.24 = 1.
(iv)

Question 4: If x + 1/x = 11, find the value of x2 +1/x2.
Solution:

Question 5: If x – 1/x = -1, find the value of x2 +1/x2.
Solution:
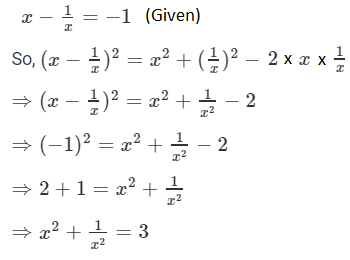
RD Sharma Solutions for Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.1
RD Sharma Solutions Class 9 Maths Chapter 4 Algebraic Identities Exercise 4.1 are based on the following algebraic Identities:
- (a + b)2 = a2 + 2ab + b2
- (a – b)2 = a2 – 2ab + b2
- (a – b)(a + b) = a2 – b2
- (x + a)(x + b) = x2 + (a + b)x + ab





Comments