Coefficient of Correlation
A coefficient of correlation is generally applied in statistics to calculate a relationship between two variables. The correlation shows a specific value of the degree of a linear relationship between the X and Y variables, say X and Y. There are various types of correlation coefficients. However, Pearson’s correlation (also known as Pearson’s R) is the correlation coefficient that is frequently used in linear regression.
Pearson’s Coefficient Correlation
Karl Pearson’s coefficient of correlation is an extensively used mathematical method in which the numerical representation is applied to measure the level of relation between linearly related variables. The coefficient of correlation is expressed by “r”.
Karl Pearson Correlation Coefficient Formula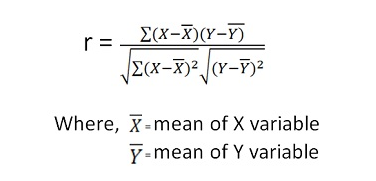
Alternative Formula (covariance formula)
Pearson correlation example
1. When a correlation coefficient is (1), that means for every increase in one variable, there is a positive increase in the other fixed proportion. For example, shoe sizes change according to the length of the feet and are perfect (almost) correlations.
2. When a correlation coefficient is (-1), that means for every positive increase in one variable, there is a negative decrease in the other fixed proportion. For example, the decrease in the quantity of gas in a gas tank shows a perfect (almost) inverse correlation with speed.
3. When a correlation coefficient is (0) for every increase, that means there is no positive or negative increase, and the two variables are not related.
Practice Questions
Actual Mean Method
| Q.1 Compute Karl Pearson’s coefficient of correlation from the following data (Use actual mean method) | |||||||
| Price (`) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| Supply (Units) | 8 | 6 | 14 | 16 | 10 | 20 | 24 |
| Q.2 Compute Karl Pearson’s coefficient of correlation from the following data: (Use actual mean method) | |||||
| X | 15 | 18 | 20 | 28 | 34 |
| Y | 40 | 42 | 46 | 50 | 52 |
Assumed Mean Method
| Q.1 Compute Karl Pearson’s coefficient of correlation from the following data: (Use assumed mean method) | |||||||
| Price (`) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| Supply (Units) | 8 | 6 | 14 | 16 | 10 | 20 | 24 |
| Q.2 From the following data, compute the correlation between the heights of father and daughter by Karl Pearson’s coefficient of correlation. (Use assumed mean method) | ||||||||
| Height of father (cm) | 65 | 66 | 67 | 67 | 68 | 69 | 71 | 73 |
| Height of daughter (cm) | 67 | 68 | 64 | 69 | 72 | 70 | 69 | 73 |
Step Deviation Method
| Q.1 Compute Karl Pearson’s coefficient of correlation from the following data: (Use step deviation method) | |||||||
| Price (`) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| Supply (Units) | 8 | 6 | 14 | 16 | 10 | 20 | 24 |
| Q.2 Compute Karl Pearson’s coefficient of correlation from the following data: (Use step deviation method) | ||||||
| Density (per sq. km) | 2000 | 5000 | 4000 | 7000 | 6000 | 3000 |
| Patients of dengue fever | 100 | 160 | 140 | 200 | 170 | 130 |
Direct Method
| Q.1 Compute Karl Pearson’s coefficient of correlation from the following data: (Use direct method) | |||||||
| Price (`) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| Supply (Units) | 8 | 6 | 14 | 16 | 10 | 20 | 24 |
| Q.2 Compute Karl Pearson’s coefficient of correlation from the following data: (Use direct method) | |||||
| Price (in `) | 5 | 6 | 3 | 4 | 3 |
| Demand (in Units) | 10 | 10 | 12 | 11 | 12 |
This concludes our article on the topic of Coefficient of Correlation, which is an important topic for Commerce students. For more such interesting articles, stay tuned to BYJU’S.
Other Important Topics in Economics
Frequently Asked Questions on Karl Pearson’s Coefficient of Correlation
What is another name for the Correlation Coefficient?
Correlation coefficient is also known as Pearson’s correlation or Pearson’s R.
What are the assumptions of Karl Pearson’s method?
The following are the assumptions of the Karl Pearson’s method:
- Level of measurement
- Related pairs
- Absence of outliers
- Linearity
How is Karl Pearson’s coefficient of correlation defined?
Karl Pearson’s coefficient of correlation is defined as a linear correlation coefficient that falls in the value range of -1 to +1. Value of -1 signifies strong negative correlation while +1 indicates strong positive correlation.
easy to study