MSBSHSE Solutions For Class 9 Maths Part 1 Chapter 3 Polynomials, are provided here in PDF format, which can be downloaded for free. The Maharashtra Board Textbook Solutions for the chapter Polynomials have been designed accurately by mathematics experts at BYJU’S. All these solutions are provided by considering the new pattern of MSBSHSE, so that students can get thorough knowledge for their exams. Chapter 3 of the MSBSHSE Solutions for Class 9 Maths helps the students in learning different terms related to polynomials. They can also learn different methods to find the degrees of the given polynomial. Besides, students can get knowledge about how to use synthetic division for finding the remainder. These solutions provided by BYJU’S cover all these concepts with detailed explanations.

Download the PDF of Maharashtra Solutions For Class 9 Maths Part 1 Chapter 3 Polynomials

Access answers to Maths MSBSHSE Solutions For Class 9 Part 1 Chapter 3 – Polynomials

Practice set 3.1 Page no: 39

1. State whether the given algebraic expressions are polynomials? Justify.
i. y + 1/y
ii. 2-5√x
iii. x² + 7x + 9
iv. 2m^-2 + 7m – 5
v. 10

Solution:

(i) Given y + 1/y

y + 1/y is not a polynomial because in this given equation the second term becomes 1 × y^-1 where -1 is not a whole number. So, the given algebraic expression is not a polynomial.

(ii) Given 2-5√x

2-5√x is not a polynomial because again the power of x is 1/2 which is not a whole number.

(iii) Given x² + 7x + 9

The given algebraic expression is a polynomial in one variable because all the powers of x are whole numbers.

(iv) Given 2m^-2 + 7m – 5

This expression is not polynomial because the power of the first term is -2 which is not a whole number.

(v) Given 10

The number 10 is a polynomial because 10 can be represented as follows: 10 × x⁰ which is equal to 10. So, it is a polynomial.

2. Write the coefficient of in each of the given polynomial.
i. m³
ii.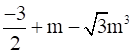 

iii.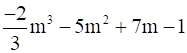 

Solution:

i. Given m³

The coefficient of any variable is the constant with which the variable is multiplied with. So, the coefficient of m³ is one.

ii. In the given question,

The coefficient of m⁰ = -3/2

The coefficient of m = 1

The coefficient of m³ = -√3

iii. In the given question,

The coefficient of m⁰ = -1

The coefficient of m¹ = 7

The coefficient of m² = -5

The coefficient of m³ = -2/3

3. Write the polynomial in x using the given information.
i. Monomial with degree 7
ii. Binomial with degree 35
iii. Trinomial with degree 8

Solution:

i. A polynomial is said to be monomial if it contains only one term in its entire expression. So, the polynomial is as follows:

7x⁷

ii. A polynomial is said to be binomial if it contains only two term in its entire expression. So, the polynomial is as follows:

2x³⁵ + 7

iii. A polynomial is said to be trinomial if it contains only three term in its entire expression. So, the polynomial is as follows:

2x⁸ + 7x + 3

4. Write the degree of the given polynomials.
i. √5
ii. x⁰
iii. x²
iv.  √2m¹⁰ – 7
v. 20 – √7
vi. 7y – y³ + y⁵
vii. x y z + x y
viii. m³n⁷ – 3m⁵n + m n

Solution:

i. The degree of a polynomial is the highest degree of its monomials (individual terms) with non-zero coefficients. This algebraic expression has zero degree.

ii. The degree of the given polynomial is zero.

iii. The degree of the given polynomial is two.

iv. The degree of the given polynomial is ten.

v. The degree of the given polynomial is one.

vi. The degree of the given polynomial is five.

vii. The degree of the given polynomial is three.

viii. The degree of the given polynomial is ten.

5. Classify the following polynomials as linear, quadratic and cubic polynomial.
i. 2x² + 3x +1
ii. 5p
iii.  √2y – ½
iv. m³ + 7m²+ 5/2 m – √7
v. a²
vi. 3r³

Solution:

i. A polynomial is said to be quadratic if the highest power of the variable in the polynomial is two.

So, this polynomial is quadratic.

ii. The given polynomial is linear as the highest power of the variable is one.

iii. This polynomial is a linear one as the variable has the highest degree as one

iv. This polynomial is a cubic polynomial because the highest power of the variable is three.

v. A polynomial is said to be quadratic if the highest power of the variable in the polynomial is two.

So, this polynomial is quadratic.

vi. This polynomial is a cubic polynomial because the highest power of the variable is three.

6. Write the following polynomials in standard form.

i. m³ + 3 + 5m
ii.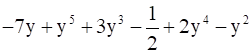 

Solution:

i. In the standard form of any polynomial it is necessary for the power of the variable to go in descending order for each term.

So, the standard form of this polynomial is as follows:

m³ + 5m + 3

ii. In the standard form of any polynomial it is necessary for the power of the variable to go in descending order for each term that is first term should consist of variable with highest power, second term should contain the variable with second highest power and so on.

So, the standard form of this polynomial is as follows:

y⁵ + 2y⁴ + 3y³ –y² -7y – ½

7. Write the following polynomials in coefficient form.

i. x³ – 2
ii. 5y
iii. 2m⁴ – 3m² + 7
iv. -2/3

Solution:

i. In the coefficient form of the polynomial, the coefficient of each term of the variable present or absent is written inside the simple brackets. So, the coefficient form is as follows:

⇒ x³ -2 = x³ + 0x² + 0x – 2

∴ The given polynomial in coefficient form is:

(1, 0, 0, -2)

ii. In the coefficient form of the polynomial, the coefficient of each term of the variable present or absent is written inside the simple brackets. So, the coefficient form is as follows:

⇒ 5y = 5.y + 0

Therefore, the given polynomial in coefficient form is:

(5, 0)

iii. In the coefficient form of the polynomial, the coefficient of each term of the variable present or absent is written inside the simple brackets. So, the coefficient form is as follows

2m⁴ – 3m² + 7 = 2.m⁴ + 0.m³ – 3.m² + 0.m + 7

Therefore, the given polynomial in coefficient form is:

(2, 0, -3, 0, 7)

iv. In the coefficient form of the polynomial, the coefficient of each term of the variable present or absent is written inside the simple brackets.

Now in this case all the powers of the variable are zero and only the constant is present.

So, the coefficient form is as follows:

(-2/3)

8. Write the polynomials in index form.
i. (1, 2, 3)
ii. (5, 0, 0, 0, -1)
iii. (-2, 2, -2, 2)

Solution:

i. The given representation is the coefficient form of the polynomial. So, the first coefficient denotes the highest power of the variable.

Writing in the index form, the polynomial is:

⇒ 1.x³ + 2x² + 0.x + 3

⇒ x³ + 2x² + 3

∴ Index form of polynomial is x³ + 2x² + 3

ii. The given representation is the coefficient form of the polynomial. So, the first coefficient denotes the highest power of the variable and the power of last term is always zero.

= 5.x⁴ +0.x³ + 0.x² + 0.x – 1

= 5x⁴ – 1

Therefore, the index form of the polynomial is = 5x⁴ – 1

iii. The given representation is the coefficient form of the polynomial. So, the first coefficient denotes the highest power of the variable and the power of last term is always zero.

= -2.x³ + 2.x² – 2.x + 2

= -2x³ + 2x² – 2x + 2

Therefore, the index form of the polynomial is = -2x³ + 2x² – 2x + 2

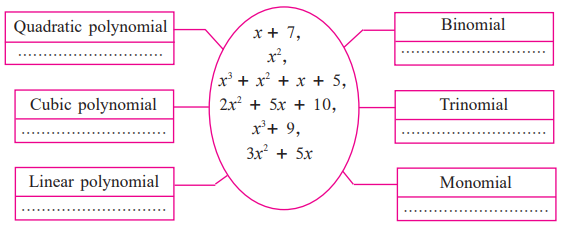
9. Write the appropriate polynomials in the boxes.

Solution:

A polynomial is said to be quadratic if the highest power of the variable in the polynomial is two.

The polynomial is said to be linear if the variable has the highest degree as one.

The polynomial is said to be cubic if the variable has the highest degree as three.

A polynomial is said to be monomial if it contains only one term in its entire expression.

A polynomial is said to be binomial if it contains only two terms in its entire expression.

A polynomial is said to be trinomial if it contains only three terms in its entire expression.

i. Quadratic polynomial: x²; 2x² + 5x + 10; 3x² + 5x

ii. Cubic polynomial: x³ + x² + x + 5; x³ + 9

iii. Linear polynomial: x + 7

iv. Binomial: x + 7; x³ + 9; 3x² + 5x

v. Trinomial: 2x² + 5x + 10

vi. Monomial: x²

Practice set 3.2 Page no: 43

1. Use the given letters to write the answer.
i. There are ‘a’ trees in the village Lat. If the number of trees increases every year by ‘b’, then how many trees will there be after ‘x’ years?
ii. For the parade there are y students in each row and x such row is formed. Then, how many students are there for the parade in all?
iii. The tens and units place of a two-digit number is m and n respectively. Write the polynomial which represents the two-digit number.

Solution:

i. Given,

Total number of trees in the village = a

Increase in the number of trees by = b

Now we have to find number of trees after x years

Number of trees in x years = (a + b) x

ii. Given,

Number of students in each row = y

Number of rows of Students = x

So total number of students = x × y

= xy

iii. For a number in tens place should be multiplied with ten and for the number in units place should be multiplied by one. So, the number that can be formed as follows:

Since m is in tens place and n is in units place,

10 × m + 1 × n

10m + n

So, the polynomial representing the two digit number is = 10m + n

2. Add the given polynomials.
i. x³ – 2x² – 9; 5x³ + 2x + 9
ii. -7m⁴+ 5m³ + √2; 5m⁴ – 3m³ + 2m² + 3m – 6
iii. 2y² + 7y + 5; 3y + 9; 3y² – 4y – 3

Solution:

i. Given (x³ – 2x² – 9) + (5x³ + 2x + 9)

= x³ – 2x² – 9 + 5x³ + 2x + 9

now by taking the like terms we get

= x³ + 5x³ – 2x² + 2x – 9 + 9

on simplifying we get

= 6x³ – 2x² + 2x

ii. Given (-7m⁴ + 5m³ + √2) + (5m⁴ – 3m³ + 2m² + 3m – 6)

= -7m⁴ + 5m³ + √2 + 5m⁴ – 3m³ + 2m² + 3m – 6

now by taking the like terms we get

= -7m⁴ + 5m⁴ + 5m³ – 3m³ + 2m² + 3m +√2 – 6

on simplifying we get

= -2m⁴ + 2m³ + 2m² + 3m + √2 – 6

iii. (2y² + 7y + 5) + (3y + 9) + (3y² – 4y – 3)

= 2y² + 7y + 5 + 3y + 9 + 3y² – 4y – 3

now by taking the like terms we get

= 2y² + 3y² + 7y + 3y – 4y + 5 + 9 – 3

on simplifying we get

= 5y² + 6y + 11

3. Subtract the second polynomial from the first.

i. x² – 9x + √3; – 19x + √3 + 7x²

ii. 2ab² + 3a²b – 4ab; 3ab – 8ab² + 2a²b

Solution:

i. In the subtraction process, the sign of the subtrahend that is the second polynomial is inverted and then the operation is carried out.

Given x² – 9x + √3 -(- 19x + √3 + 7x²)

= x² – 9x + √3 + 19x – √ 3 – 7x²

= x² – 7x² – 9x + 19x + √3 – √3

= – 6x² + 10x

ii. In the subtraction process, the sign of the subtrahend that is the second polynomial is inverted and then the operation is carried out.

Given (2ab² + 3a²b – 4ab) – (3ab – 8ab² + 2a²b)

= 2ab² + 3a²b – 4ab – 3ab + 8ab² – 2a²b

= 2ab² + 8ab² + 3a²b – 2a²b – 4ab – 3ab

= 10ab² + a²b – 7ab

4. Multiply the given polynomials.
i. 2x; x² – 2x
ii. x⁵ – 1; x³ + 2x³ + 2
iii. 2y + 1; y² – 2y³ + 3y

Solution:

The multiplication is as follows:

⇒ 2x × (x² – 2x – 1)

⇒ 2x.x² – 2x.2x – 2x.1

⇒ 2x²⁺¹ – 4x¹⁺¹ – 2x

⇒ 2x³ – 4x² – 2x

Therefore, the product = 2x³ – 4x² – 2x

ii. The multiplication is as follows:

⇒ (x⁵ – 1) × (x³ + 2x³ + 2)

⇒ x⁵.x³ + 2x³.x⁵ + 2.x⁵ – 1.x³ – 1.2x³ – 1.2

⇒ x⁵⁺³ + 2x^{3 + 5} +2x⁵ – x³ – 2x³ – 2

⇒ x⁸ + 2x⁸ + 5 + 2x⁵ – x³ – 2x³ – 2

⇒ 3x⁸ + 2x⁵ + 3x³ + 3

The product is = 3x⁸ + 2x⁵ + 3x³ + 3

iii. The multiplication is as follows:

⇒ (2y + 1) × (y² – 2y³ + 3y)

⇒ 2y.y² – 2y³.2y + 3y.2y + 1.y² – 1.2y³ + 1.3y

⇒ 2y²⁺¹ – 4y³⁺¹ + 6y¹⁺¹ + y² – 2y³ + 3y

⇒ 2y³ – 4y⁴ + 6y² + y² – 2y³ + 3y

⇒ -4y⁴ + 7y² + 3y

The product is = -4y⁴ + 7y² + 3y

5. Divide first polynomial by second polynomial and write the answer in the form ‘Dividend = Divisor × Quotient + Remainder’.
i. x³ – 64; x – 4
ii. 5x⁵ + 4x⁴ – 3x³ + 2x² + 2; x² – x

Solution:

i. x³ – 64 = x3 + 0x² + 0x – 64

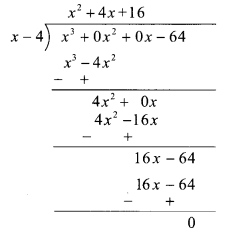
∴ Quotient = x² + 4x + 16, Remainder = 0

Now, Dividend = Divisor x Quotient + Remainder

∴ x³ – 64 = (x – 4) (x² + 4x + 16) + 0

ii. 5x⁵ + 4x⁴ – 3x³ + 2x² + 2 = 5x⁵ + 4x⁴ – 3x³ + 2x + 0x + 2

∴ Quotient = 5x³ + 9x² + 6x + 8,

Remainder = 8x + 2

Now, Dividend = Divisor x Quotient + Remainder

∴ 5x⁵ + 4x⁴ – 3x³ + 2x² + 2 = (x² – x) (5x³ + 9x² + 6x + 8) + (8x + 2)

6. Write down the information in the form of algebraic expression and simplify.

There is a rectangular farm with length (2a² + 3b²) meter and breadth (a² + b²) meter. The farmer used a square shaped plot of the farm to build a house. The side of the plot was (a² – b²) meter. What is the area of the remaining part of the farm?

Solution:

Length of the rectangular farm = (2a² + 3b²) m

Breadth of the rectangular farm = (a² + b²) m

Area of the farm = length x breadth = (2a² + 3b²) x (a² + b²)

= 2a²(a² + b²) + 3b²(a² + b²)

= 2a² + 2a²b² + 3a²b² + 3b⁴

= (2a⁴ + 5a²b² + 3b⁴) sq. m … (i)

The farmer used a square shaped plot of the farm to build a house.

Side of the square shaped plot = (a² – b²) m

∴ Area of the plot = (side)²

= (a² – b²)²

= (a⁴ – 2a²b² + b⁴) sq m… .(ii)

∴ Area of the remaining farm = Area of the farm – Area of the plot

= (2a⁴ + 5a²b² + 3b⁴) – (a⁴ – 2a²b² + b⁴) … [From (i) and (ii)]

= 2a⁴ + 5a²b² + 3b⁴ – a⁴ + 2a²b² – b⁴

= 2a⁴ – a⁴ + 5a²b² + 2a²b² + 3b⁴ – b⁴

= a⁴ + 7a²b² + 2b⁴

∴ The area of the remaining farm is (a⁴ + 7a²b² + 2b⁴) sq. m.

Practice set 3.3 Page no: 46

1. Divide each of the following polynomials by synthetic division method and also by linear division method. Write the quotient and the remainder.
i. (2m² – 3m + 10) ÷ (m – 5)
ii. (x⁴ + 2x³ + 3x² + 4x + 5) ÷ (x + 2)
iii. (y³ – 216) ÷ (y – 6)
iv. (2x⁴ + 3x³ + 4x – 2x²) ÷ (x + 3)
v. (x⁴ – 3x² – 8) ÷ (x + 4)
vi. (y³ – 3y² + 5y – 1) ÷ (y – 1)

Solution:

i. Synthetic division:

(2m² – 3m + 10) ÷ (m – 5)

Dividend = 2m² – 3m + 10

∴ Coefficient form of dividend = (2, -3, 10)

Divisor = m – 5

∴ Opposite of -5 is 5.

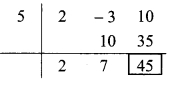
Coefficient form of quotient = (2, 7)

∴ Quotient = 2m + 7,

Remainder = 45

Linear division method:

2m² – 3m + 10

To get the term 2m², multiply (m – 5) by 2m and add 10m,

= 2m(m – 5) + 10m- 3m + 10

= 2m(m – 5) + 7m + 10

To get the term 7m, multiply (m – 5) by 7 and add 35

= 2m(m – 5) + 7(m- 5) + 35+ 10

= (m – 5) (2m + 7) + 45

∴ Quotient = 2m + 7,

Remainder = 45

ii. Synthetic division:

(x⁴ + 2x³ + 3x² + 4x + 5) ÷ (x + 2)

Dividend = x⁴ + 2x³ + 3x² + 4x + 5

∴ Coefficient form of dividend = (1, 2, 3, 4, 5)

Divisor = x + 2

∴ Opposite of + 2 is -2.

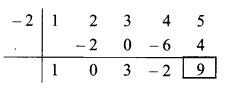
Coefficient form of quotient = (1, 0, 3, -2)

∴ Quotient = x³ + 3x – 2,

Remainder = 9

Linear division method:

x⁴ + 2x³ + 3x² + 4x + 5

To get the term x⁴, multiply (x + 2) by x³ and subtract 2x³,

= x³(x + 2) – 2x³ + 2x³ + 3x² + 4x + 5

= x³(x + 2) + 3x² + 4x + 5

To get the term 3x², multiply (x + 2) by 3x and subtract 6x,

= x³(x + 2) + 3x(x + 2) – 6x + 4x + 5

= x³(x + 2) + 3x(x + 2) – 2x + 5

To get the term -2x, multiply (x + 2) by -2 and add 4,

= x³(x + 2) + 3x(x + 2) – 2(x + 2) + 4 + 5

= (x + 2) (x3 + 3x – 2) + 9

∴ Quotient = x³ + 3x – 2,

Remainder – 9

iii. Synthetic division:

(y³ – 216) ÷ (y – 6)

Dividend = y³ – 216

∴ Index form = y³ + 0y³ + 0y – 216

∴ Coefficient form of dividend = (1, 0, 0, -216)

Divisor = y – 6

∴ Opposite of – 6 is 6.

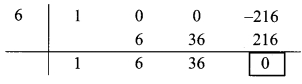
Coefficient form of quotient = (1, 6, 36)

∴ Quotient = y² + 6y + 36,

Remainder = 0

Linear division method:

y³ – 216

To get the term y³, multiply (y – 6) by y² and add 6y²,

= y²(y – 6) + 6y² – 216

= y²(y – 6) + 6ysup>2 – 216

To get the, term 6 y² multiply (y – 6) by 6y and add 36y,

= y²(y – 6) + 6y(y – 6) + 36y – 216

= y²(y – 6) + 6y(y – 6) + 36y – 216

To get the term 36y, multiply (y- 6) by 36 and add 216,

= y² (y – 6) + 6y(y – 6) + 36(y – 6) + 216 – 216

= (y – 6) (y² + 6y + 36) + 0

Quotient = y² + 6y + 36

Remainder = 0

iv. Synthetic division:

(2x⁴ + 3x³ + 4x – 2x²) ÷ (x + 3)

Dividend = 2x⁴ + 3x³ + 4x – 2x²

∴ Index form = 2x⁴ + 3x³ – 2x² + 4x + 0

∴ Coefficient form of the dividend = (2,3, -2,4,0)

Divisor = x + 3

∴ Opposite of + 3 is -3

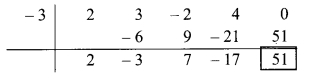
Coefficient form of quotient = (2, -3, 7, -17)

∴ Quotient = 2x³ – 3x² + 7x – 17,

Remainder = 51

Linear division method:

2x⁴ + 3x³ + 4x – 2x² = 2x² + 3x³ – 2x² + 4x

To get the term 2x⁴, multiply (x + 3) by 2x³ and subtract 6x³,

= 2x³(x + 31 – 6x³ + 3x³ – 2x² + 4x

= 2x³(x + 3) – 3x³ – 2x² + 4x

To get the term – 3x³, multiply (x + 3) by -3x² and add 9x²,

= 2x³(x + 3) – 3x²(x + 3) + 9x² – 2x² + 4x

= 2x³(x + 3) – 3x²(x + 3) + 7x² + 4x

To get the term 7x², multiply (x + 3) by 7x and subtract 21x,

= 2x³(x + 3) – 3x²(x + 3) + 7x(x + 3) – 21x + 4x

= 2x³(x + 3) – 3x²(x + 3) + 7x(x + 3) – 17x

To get the term -17x, multiply (x + 3) by -17 and add 51,

= 2x³(x + 3) – 3x²(x + 3) + 7x(x+3) – 17(x + 3) + 51

= (x + 3) (2x³ – 3x² + 7x- 17) + 51

∴ Quotient = 2x³ – 3x² + 7x – 17,

Remainder = 51

v. Synthetic division:

(x⁴ – 3x² – 8) + (x + 4)

Dividend = x⁴ – 3x² – 8

∴ Index form = x⁴ + 0x³ – 3x² + 0x – 8

∴ Coefficient form of the dividend = (1,0, -3,0, -8)

Divisor = x + 4

∴ Opposite of + 4 is -4

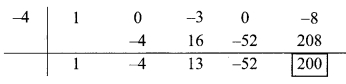
∴ Coefficient form of quotient = (1, -4, 13, -52)

∴ Quotient = x³ – 4x² + 13x – 52,

Remainder = 200

Linear division method:

x⁴ – 3x² – 8

To get the term x⁴, multiply (x + 4) by x³ and subtract 4x³,

= x³(x + 4) – 4x³ – 3x² – 8

= x³(x + 4) – 4x³ – 3x² – 8

To get the term – 4x³, multiply (x + 4) by -4x² and add 16x²,

= x³(x + 4) – 4x² (x + 4) + 16x² – 3x² – 8

= x³(x + 4) – 4x² (x + 4) + 13x² – 8

To get the term 13x², multiply (x + 4) by 13x and subtract 52x,

= x³(x + 4) – 4x²(x + 4) + 13x(x + 4) – 52x – 8

= x³(x + 4) – 4x²(x + 4) + 13x(x + 4) – 52x – 8

To get the term -52x, multiply (x + 4) by – 52 and add 208,

= x³(x + 4) – 4x²(x + 4) + 13x(x + 4) – 52(x + 4) + 208 – 8

= (x + 4) (x³ – 4x² + 13x – 52) + 200

∴ Quotient = x³ – 4x² + 13x – 52,

Remainder 200

vi. Synthetic division:

(y³ – 3y² + 5y – 1) ÷ (y – 1)

Dividend = y³ – 3y² + 5y – 1

Coefficient form of the dividend = (1, -3, 5, -1)

Divisor = y – 1

∴Opposite of -1 is 1.

∴ Coefficient form of quotient = (1, -2, 3)

∴ Quotient = y² – 2y + 3,

Remainder = 2

Linear division method:

y³ -3y² + 5y – 1

To get the term y³ , multiply (y – 1) by y² and add y²

= y² (y – 1) + y² – 3y² + 5y – 1

= y² (y – 1) – 2y² + 5y – 1

To get the term -2y², multiply (y – 1) by -2y and subtract 2y,

= y² (y – 1) – 2y(y – 1) – 2y + 5y – 1

= y² (y – 1) – 2y(y – 1) + 3y – 1

To get the term 3y, multiply (y – 1) by 3 and add 3,

= y² (y – 1) – 2y(y – 1) + 3(y- 1) + 3 – 1

= (y – 1)(y² – 2y + 3) + 2

∴ Quotient = y² – 2y + 3,

Remainder = 2.

Practice set 3.4 Page no: 48

1. For x = 0, find the value of the polynomial x² – 5x + 5.

Solution:

p(x) = x² – 5x + 5

Put x = 0 in the given polynomial.

∴ p (0) = (0)² – 5(0) + 5

= 0 – 0 + 5

∴ p (0) = 5

2. If p(y) = y² – 3√2 + 1, then find p (3√2).

Solution:

p(y) = y² – 3√2 y + 1

Put p= 3√2 in the given polynomial.

∴ p( 3√2 ) = (3√2 )² – 3√2 (3√2 ) + 1

= 9 x 2 – 9 x 2 + 1

= 18 – 18 + 1

∴ p( 3√2 ) = 1

3. If p(m) = m³ + 2m² – m + 10, then P(a) + p(-a) =?

Solution:

p(m) = m³ + 2m² – m + 10

Put m = a in the given polynomial.

∴ p(a) = a³ + 2a² – a + 10 …(i)

Put m = -a in the given polynomial.

p(-a) = (-a)³ + 2(-a)² – (-a) +10

∴ p (-a) = -a³ + 2a² + a + 10 …(ii)

Adding (i) and (ii),

p(a) + p(-a) = (a³ + 2a² – a + 10) + (-a³ + 2a² + a + 10)

= a³ – a³ + 2a² + 2a² – a + a + 10 + 10

∴ p(a) + p(-a) = 4a² + 20

4. If p(y) = 2y³ – 6y² – 5y + 7, then find p (2).

Solution:

p(y) = 2y³ – 6y² – 5y + 7

Put y = 2 in the given polynomial.

∴ p(2) = 2(2)³ – 6(2)² – 5(2) + 7

= 2 x 8 – 6 x 4 – 10 + 7

= 16 – 24 – 10 + 7

∴ P(2) = -11

Practice set 3.5 Page no: 53

1. Find the value of the polynomial 2x – 2x³ + 7 using given values for x.
i. x = 3
ii. x = -1
iii. x = 0
Solution:

i. let p(x) = 2x – 2x³ + 7

Put x = 3 in the given polynomial.

∴ p (3) = 2(3) – 2(3)³ + 7

= 6 – 2 x 27 + 7

= 6 – 54 + 7

∴ p (3) = – 41

ii. let p(x) = 2x – 2x³ + 7

Put x = -1 in the given polynomial.

∴ p(- 1) = 2(- 1) – 2(-1)³ + 7

= – 2 – 2(-1) + 7

= -2 + 2 + 7

∴ p(-1) = 7

iii. let p(x) = 2x – 2x³ + 7

Put x = 0 in the given polynomial.

∴ p (0) = 2(0) – 2(0)³ + 7

= 0 – 0 + 7

∴ p (0) = 7

2. For each of the following polynomial, find p (1), p (0) and p (- 2).
i. p(x) = x³
ii. p(y) = y² – 2y + 5
iii. p(y) = x⁴ – 2x² + x

Solution:

i. p(x) = x³

∴ p (1) = 1³ = 1

p(x) = x³

∴ p (0) = 0³ = 0

p(x) = x³

∴ p(-2) = (-2)³ = -8

ii. p(y) = y² – 2y + 5

∴ p(1) = 1² – 2(1) + 5

= 1 – 2 + 5

∴ P(1) = 4

p(y) = y² – 2y + 5

∴ p(0) = 0² – 2(0) + 5

= 0 – 0 + 5

∴ p(0) = 5

p(y) = y² – 2y + 5

∴ p(- 2) = (- 2)² – 2(- 2) + 5

= 4 + 4 + 5

∴ p(-2) = 13

iii. p(x) = x⁴ – 2x² – x

∴ p(1) = (1)⁴ – 2(1)² – 1

= 1 – 2 – 1

∴ p(1) = -2

∴ p(x) = x⁴ – 2x² – x

∴ p(0) = (0)⁴ – 2(0)² – 0

= 0 – 0 – 0

∴ p(0) = 0

p(x) = x⁴ – 2x² – x

∴ p(-2) = (-2)⁴ – 2(-2)² – (-2)

= 16 – 2(4) + 2

= 16 – 8 + 2

∴ p(-2) = 10

3. If the value of the polynomial m³ + 2m + a is 12 for m = 2, then find the value of a.

Solution:

Given p(m) = m³ + 2m + a

If m = 2 then,

∴ p (2) = (2)³ + 2(2) + a

∴ 12 = 8 + 4 + a … [∵ p(2)= 12]

∴ 12 = 12 + a

∴ a = 12 – 12

∴ a = 0

4. For the polynomial mx² – 2x + 3 if p (-1) = 7, then find m.

Solution:

Given

p(x) = mx² – 2x + 3

If m = -1

∴ p (- 1) = m (- 1)² – 2(- 1) + 3

∴ 7 = m (1) + 2 + 3 … [∵ p(-1) = 7]

∴ 7 = m + 5

∴ m = 7 – 5

∴ m = 2

5. Divide the first polynomial by the second polynomial and find the remainder using remainder theorem.
i. (x² – 1x + 9); (x + 1)
ii. (2x³ – 2x² + ax – a); (x – a)
iii. (54m³ + 18m² – 27m + 5); (m – 3)

Solution:

i. p(x) = x² – 7x + 9

Divisor = x + 1

∴ take x = – 1

∴ By remainder theorem,

∴ Remainder =p(-1)

p(x) = x² – 7x + 9

∴ p(-1) = (- 1)² – 7(- 1) + 9

= 1 + 7 + 9

∴ Remainder =17

ii. p(x) = 2x³ – 2x² + ax – a

Divisor = x – a

∴ take x = a

By remainder theorem,

Remainder = p(a)

p(x) = 2x³ – 2x² + ax – a

∴ p(a) = 2a³ – 2a² + a(a) – a

= 2a³– 2a² + a² – a

∴ Remainder = 2a³ – a² – a

iii. p(m) = 54m³ + 18m² – 27m + 5

Divisor = m – 3

∴ take m = 3

∴ By remainder theorem,

Remainder = p(3)

p(m) = 54m³ + 18m² – 27m + 5

∴ p(3) = 54(3)³ +18(3)² – 27(3) + 5

= 54(27) + 18(9) – 81 + 5

= 1458 + 162 – 81 + 5

∴ Remainder = 1544

6. If the polynomial y³ – 5y² + 7y + m is divided by y + 2 and the remainder is 50, then find the value of m.

Solution:

let p(y) = y³ – 5y² + 7y + m

Divisor = y + 2

∴ take y = – 2

∴ By remainder theorem,

Remainder = p(- 2) = 50

P(y) = y³ – 5y² + 7y + m

∴ P(-2) = (- 2)³ – 5(- 2)² + 7(- 2) + m

∴ 50 = -8 – 5(4) – 14 + m

∴ 50 = -8 – 20 – 14 + m

∴ 50 = – 42 + m

∴ m = 50 + 42

∴ m = 92

7. Use factor theorem to determine whether x + 3 is a factor of x² + 2x – 3 or not.

Solution:

p(x) = x² + 2x – 3

Divisor = x + 3

∴ take x = – 3

∴ Remainder = p(-3)

p(x) = x² + 2x – 3

∴ p(-3) = (-3)² + 2(- 3) – 3

= 9 – 6 – 3

∴ p(-3) = 0

∴ By factor theorem, x + 3 is a factor of x² + 2x – 3.

Practice set 3.6 Page no: 54

1. Find the factors of the polynomials given below.
i. 2x² + x – 1
ii. 2m² + 5m – 3
iii. 12x² + 61x + 77
iv. 3y² – 2y – 1
v. √3x² + 4x + √3
vi. ½ x² – 3x + 4

Solution:

(i) Given 2x² + x – 1

⟹ 2x² + 2x – x – 1

⟹ 2x (x + 1) – 1 (x + 1)

⟹ (x + 1) (2x – 1)

Therefore, the factors of the given polynomial = (x + 1) (2x – 1)

ii. Given 2m² + 5m – 3

= 2m² + 6m – m – 3

= 2m (m + 3) – 1(m + 3)

Therefore, the factors of the given polynomial = (m + 3) (2m – 1)

iii. Given 12x² + 61x + 77

= 12x² + 28x + 33x + 77

= 4x (3x + 7) 4 + 11(3x + 7)

Therefore, the factors of the given polynomial = (3x + 7) (4x + 11)

iv. Given 3y² – 2y – 1

= 3y² – 3y + y – 1

= 3y (y – 1) + 1 (y – 1)

Therefore, the factors of the given polynomial = (y – 1) (3y + 1)

v. Given √3×2 + 4x + √3

= √3×2 + 3x + x + √3

= √3×2 + √3 x √3x + x + √3

= √3x(x + √3) + 1 ( x + √3 )

Therefore, the factors of the given polynomial = (x + √3)(√3x + 1)

vi. Given 1/2 x² – 3x + 1

⟹ 1/2x² – 2x – x + 4

⟹ 1/2x (x – 4) – 1 (x – 4)

⟹ (x – 4) (1/2x – 1)

Therefore, the factors of the given polynomial = (x – 4) (1/2x – 1)

2. Factorize the following polynomials.

i. (x² – x)² – 8(x² – x) + 12

iii. (x² – 6x)² – 8(x² – 6x + 8) – 64

v. (y + 2) (y – 3) (y + 8) (y + 3) + 56

vii. (x – 3) (x – 4)² (x – 5) – 6

Solution:

i. (x² – x)² – 8(x² – x) + 12

= m² – 8m + 12 …[Putting x² – x = m]

= m² – 6m – 2m + 12

= m(m – 6) – 2(m – 6)

= (m – 6)(m – 2)

= (x² – x- 6) (x² – x- 2) …[Replacing m = x² -x]

= (x² – 3x + 2x – 6) (x² – 2x + x – 2)

= [x(x – 3) + 2(x – 3)] [x(x – 2) + 1 (x-2)]

= (x – 3) (x + 2) (x – 2) (x + 1)

ii. (x – 5)² – (5x – 25) – 24

= (x – 5)² – (5x – 25) – 24

= (x – 5)² – 5(x – 5) – 24

= m² – 5m – 24 … [Putting x – 5 = m]

= m² – 8m + 3m – 24

= m(m – 8) + 3(m – 8)

= (m – 8) (m + 3)

= (x – 5 – 8) (x – 5 + 3) … [Replacing m = x – 5]

iii. (x² – 6x)² – 8(x² – 6x + 8) – 64

= m² – 8(m + 8)-64 …[Putting x² – 6x = m]

= m² – 8m – 64 – 64

= m² – 8m – 128

= m² – 16m + 8m- 128

= m(m – 16) + 8(m – 16)

= (m – 16)(m + 8)

= (x² – 6x – 16) (x² – 6x + 8) … [Replacing m = x² – 6x]

= (x² – 8x + 2x – 16) (x² – 4x – 2x + 8)

= [x(x – 8) + 2(x – 8)] [x(x – 4) – 2(x – 4)]

= (x – 8) (x + 2) (x – 4) (x – 2)

iv. (x²– 2x + 3) (x² – 2x + 5) – 35

= (m + 3) (m + 5) – 35 … [Putting x² – 2x = m]

= m (m + 5) + 3(m + 5) – 35

= m² + 5m + 3m + 15 – 35

= m² + 8m – 20

= m² + 10m – 2m – 20

= m(m + 10) – 2(m + 10)

= (m + 10) (m – 2)

= (x² – 2x + 10) (x² – 2x – 2) … [Replacing m = x² – 2x]

v. (y + 2) (y – 3) (y + 8) (y + 3) + 56

= (y + 2)(y + 3)(y – 3)(y + 8) + 56

= (y² + 3y + 2y + 6) (y² + 8y – 3y – 24) + 56

= (y² + 5y + 6) (y² + 5y – 24) + 56

= (m + 6) (m – 24) + 56 … [Putting y2 + 5y = m]

= m (m – 24) + 6 (m – 24) + 56

= m² – 24m + 6m – 144 + 56

= m² – 18m – 88

= m² – 22m + 4m – 88

= m(m – 22) + 4(m – 22)

= (m – 22) (m + 4)

= (y² + 5y – 22)(y² + 5y + 4) … [Replacing m = y² + 5y]

= (y² + 5y – 22) (y² + 4y + y + 4)

= (y² + 5y – 22) [y(y + 4) + 1(y + 4)]

= (y² + 5y – 22) (y + 4) (y + 1)

vi. (y² + 5y) (y² + 5y – 2) – 24

= (m)(m – 2) – 24 … [Putting y² + 5y = m]

= m² – 2m – 24

= m² – 6m + 4m – 24

= m(m – 6) + 4(m – 6)

= (m – 6) (m + 4)

= (y² + 5y – 6) (y² + 5y + 4) … [Replacing m = y² + 5y]

= (y² + 6y – y – 6) (y² + 4y + y + 4)

= [y(y + 6) – 1(y + 6)] [y(y + 4) + 1(y + 4)]

= (y + 6) (y – 1) (y + 4) (y + 1)

vii. (x – 3) (x – 4)2 (x – 5) – 6

= (x – 3) (x – 5) (x – 4)² – 6

= (x² – 5x – 3x + 15) (x² – 8x + 16) – 6

= (x² – 8x + 15) (x² – 8x + 16) – 6

= (m + 15) (m+ 16) – 6 … [Putting x² – 8x = m]

= m (m + 16) + 15 (m + 16) – 6

= m² + 16m + 15m + 240 – 6

= m² + 31m + 234

= m² + 18m + 13m + 234

= m(m + 18) + 13(m + 18)

= (m + 18) (m + 13)

= (x² – 8x + 18) (x² – 8x + 13) … [Replacing m = x² – 8x]

Problem set 3 Page no: 55

1. Write the correct alternative answer for each of the following questions.

i. Which of the following is a polynomial?

Solution:

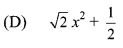
Explanation:

The option D is the only valid polynomial because in this polynomial only the power of the variable is a whole number.

ii. What is the degree of the polynomial √7?
(A) 12
(B) 5
(C) 2
(D) 0

Solution:

(D) 0

Explanation:

The degree of this polynomial is zero as √7x⁰.

iii. What is the degree of the polynomial?
(A) 0
(B) 1
(C) undefined
(D) any real number

Solution:

(C) undefined

Explanation:

Option (C) is the degree of zero polynomial as zero polynomial does not have any variable and so its degree is not defined.

iv. What is the degree of the polynomial 2x² + 5xsup>3 + 7?
(A) 3
(B) 2
(C) 5
(D) 7

Solution:

(A) 3

Explanation:

The degree of a polynomial is the highest degree of its monomials (individual terms) with non-zero coefficients.

Therefore, the degree of this polynomial is 3

v. What is the coefficient form of x³ – 1?
(A) (1, -1)
(B) (3, -1)
(C) (1, 0, 0, -1)
(D) (1, 3, -1)

Solution:

(C) (1, 0, 0, -1)

Explanation:

The coefficient form is as follows:

x³ – 1 = x³ + 0x² + 0x – 1

The coefficient form is:

(1, 0, 0, -1)

vi. p(x) = x² – x + 3, then p (7√7) =?
(A) 3
(B) 7√7
(C) 42√7+3
(D) 49√7

Solution:

(D) 49√7

Explanation:

Put p =7√7 throughout the polynomial

= (7√7)² – (7√7 × 7√7) + 3

=49 × 7 – (49 × 7) + 3

=343 – 343 + 3

=3

vii. When x = – 1, what is the value of the polynomial 2x³ + 2x ?
(A) 4
(B) 2
(C) -2
(D) -4

Solution:

(A) 4

Explanation:

Put x = -1 throughout the polynomial

= 2 × (-1)3 + (2 × -1)

= -2 -2

= -4

viii. If x – 1 is a factor of the polynomial 3x² + mx, then find the value of m.
(A) 2
(B) -2
(C) -3
(D) 3

Solution:

(C) -3

Explanation:

Put x = -1 throughout the polynomial

= 2 × (-1)3 + (2 × -1)

= -2 -2

= -4

ix. Multiply (x² – 3) (2x – 7x³ + 4) and write the degree of the product.
(A) 5
(B) 3
(C) 2
(D) 0

Solution:

(A) 5

Explanation:

The multiplication is as follows:

= (x² -3) × (2x – 7x³ + 4)

= x².2x – 7x³.x² + 4x² -3.2x + 3.7x³ -3.4

= 2.x²⁺¹ – 7x³⁺² + 4x² -6x + 21x³-12

= 2x³ – 7x⁵ + 4x² – 6x + 21x³ – 12

Therefore, the degree of the product is 5.

x. Which is the following is a linear polynomial?
(A) x + 5
(B) x² + 5
(C) x³ + 5
(D) x⁴ + 5

Solution:

(A) x + 5

Explanation:

A polynomial is said to be linear if the highest power of the variable is one. So, among the options x + 5 only has highest power as one.

2. Write the degree of the polynomial for each of the following.
i. 5 + 3x⁴
ii. 7
iii. ax⁷ + bx⁹ (a, b are constants)

Solution:

i. 5 + 3x⁴

Here, the highest power of x is 4.

∴Degree of the polynomial = 4

ii. 7 = 7x°

∴ Degree of the polynomial = 0

iii. ax⁷ + bx⁹

Here, the highest power of x is 9.

∴Degree of the polynomial = 9

3. Write the following polynomials in standard form. [1 Mark each] i. 4x² + 7x⁴ – x³ – x + 9
ii. p + 2p³ + 10p² + 5p⁴ – 8

Solution:

i. 7x⁴ – x³ + 4x² – x + 9

ii. 5p⁴ + 2p³ + 10p² + p – 8

4. Write the following polynomial in coefficient form.
i. x⁴ + 16
ii. m⁵ + 2m² + 3m+15

Solution:

i. x⁴ + 16

Index form = x⁴ + 0x³ + 0x² + 0x + 16

∴ Coefficient form of the polynomial = (1,0,0,0,16)

ii. m⁵ + 2m² + 3m + 15

Index form = m⁵ + 0m⁴ + 0m³ + 2m² + 3m + 15

∴ Coefficient form of the polynomial = (1, 0, 0, 2, 3, 15)

Polynomials are expressions which are composed of two algebraic terms. The concepts covered in the chapter Polynomials can be learnt in depth at BYJU’S. Other beneficial study materials that the students can find to prepare proficiently for the exam are the Maharashtra State Board textbooks and sample papers.