Question

A 6-kg weight is fastened to the end of a steel wire of unstreched length 60 cm. It is whirled in a vertical circle and has an angular velocity of 2 revolution per second at the bottom of the circle. The area of cross-section of the wire is $0.05c{m}^2$. The elongation of the wire when the weight is at the lowest point of the path is $(Y_{steel}=2\times {10}^{11}Pa)$

• A.
• B.
• C. 3.77 m
• D.

Answer 1

The correct option is D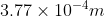

Let $l$ be the length of the at the bottommost point. $l=l_0+\Delta l$.

We have,

$\Delta l=\frac{W{l}_0}{YA}$. Also $\frac{T}{A}=\frac{YA\Delta l}{l_0}$

In the rest frame of the weight, we have at the bottommost position

$T=mg+m{\omega }^{2}l$

$\frac{YA\Delta l}{l_0}=mg+m{\omega }^2(l_0+\Delta l)$

On solving and substituting,

$\Delta l=\frac{mg+m{\omega }^2{l}_0}{\frac{YA}{l_0}-m{\omega }^2}$

$=3.77\times {10}^{-4}$m