1
Question
A certain list consists of 3 different numbers. Does the median of the 3 numbers equal the average (arithmetic mean) of the 3 numbers?
(1) The range of the 3 numbers is equal to twice the difference between the greatest number and the median.
(2) The sum of the 3 numbers is equal to 3 times one of the numbers.
A certain list consists of 3 different numbers. Does the median of the 3 numbers equal the average (arithmetic mean) of the 3 numbers?
(1) The range of the 3 numbers is equal to twice the difference between the greatest number and the median.
(2) The sum of the 3 numbers is equal to 3 times one of the numbers.
Open in App
Solution
The correct option is C Each statement alone is sufficient.
- Let the numbers be x, y, and z so that
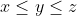 . Determine whether
. Determine whether  , or equivalently, whether 3y = x + y + z, or equivalently, whether 2y = x + z.
, or equivalently, whether 3y = x + y + z, or equivalently, whether 2y = x + z.
- Given that the range is equal to twice the difference between the greatest number and the median, it follows that z − x = 2(z − y), or z − x = 2z − 2y, or 2y = x + z; SUFFICIENT.
- Given that the sum of the 3 numbers equals 3 times one of the numbers, it follows that x + y + z = 3x or x + y + z = 3y or x + y + z = 3z. If x + y + z = 3x, then y + z = 2x, or (y − x) + (z − x) = 0. This shows two nonnegative numbers added to give zero, and hence each number must be zero. Therefore, y − x = 0 and z − x = 0, or x = y = z, and it follows that the median of the 3 numbers equals the average of the 3 numbers. If x + y + z = 3y, then x + z = 2y, and hence by the initial comments, the median of the 3 numbers equals the average of the 3 numbers. If x + y + z = 3z, then x + y = 2z, or 0 = (z − x) + (z − y). This shows two nonnegative numbers added to give zero, and hence each number must be zero. Therefore, z − x = 0 and z − y = 0, or x = y = z, and it follows that the median of the 3 numbers equals the average of the 3 numbers; SUFFICIENT.
- The correct answer is D; each statement alone is sufficient.
- Let the numbers be x, y, and z so that
. Determine whether
, or equivalently, whether 3y = x + y + z, or equivalently, whether 2y = x + z.
- Given that the range is equal to twice the difference between the greatest number and the median, it follows that z − x = 2(z − y), or z − x = 2z − 2y, or 2y = x + z; SUFFICIENT.
- Given that the sum of the 3 numbers equals 3 times one of the numbers, it follows that x + y + z = 3x or x + y + z = 3y or x + y + z = 3z. If x + y + z = 3x, then y + z = 2x, or (y − x) + (z − x) = 0. This shows two nonnegative numbers added to give zero, and hence each number must be zero. Therefore, y − x = 0 and z − x = 0, or x = y = z, and it follows that the median of the 3 numbers equals the average of the 3 numbers. If x + y + z = 3y, then x + z = 2y, and hence by the initial comments, the median of the 3 numbers equals the average of the 3 numbers. If x + y + z = 3z, then x + y = 2z, or 0 = (z − x) + (z − y). This shows two nonnegative numbers added to give zero, and hence each number must be zero. Therefore, z − x = 0 and z − y = 0, or x = y = z, and it follows that the median of the 3 numbers equals the average of the 3 numbers; SUFFICIENT.
- The correct answer is D; each statement alone is sufficient.
Suggest Corrections
0
View More
Join BYJU'S Learning Program
Join BYJU'S Learning Program
