14
Question
A hollow cylinder, a spherical shell, a solid cylinder and a solid sphere are allowed to roll on a inclined rough surface of coefficient of friction μ and inclination θ. The correct statements are
A hollow cylinder, a spherical shell, a solid cylinder and a solid sphere are allowed to roll on a inclined rough surface of coefficient of friction μ and inclination θ. The correct statements are
Open in App
Solution
The correct options are
A if all the objects are rolling and have same mass, the K.E. of all the objects will be same at the bottom of inclined plane
B if cylindrical shell can roll on inclined plan, all other objects will also roll
C work done by the frictional force will be zero, if objects are rolling

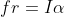
to satisfy the condition of pure rolling 
solving this
since  therefore max
therefore max  thus for cylindrical shell as we know k = 1 which is maximium of all three therefore maximium
thus for cylindrical shell as we know k = 1 which is maximium of all three therefore maximium 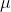 is offered by the plane and for other two
is offered by the plane and for other two 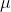 is enough to make them roll.
is enough to make them roll.
Work done by friction is always 0 in the case of rolling as we know that point of contact is always at rest.
Applying the conservation of mechanical energy

that total K.E = mghalso 
A if all the objects are rolling and have same mass, the K.E. of all the objects will be same at the bottom of inclined plane
B if cylindrical shell can roll on inclined plan, all other objects will also roll
C work done by the frictional force will be zero, if objects are rolling
to satisfy the condition of pure rolling
solving this
since 
therefore max 
thus for cylindrical shell as we know k = 1 which is maximium of all three therefore maximium 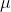 is offered by the plane and for other two
is offered by the plane and for other two 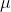 is enough to make them roll.
is enough to make them roll.
Work done by friction is always 0 in the case of rolling as we know that point of contact is always at rest.
Applying the conservation of mechanical energy
that total K.E = mgh
also 
Suggest Corrections
0
