1
Question
A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a so that it slides a distanced down the wall making an angle β with the horizontal, then
A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a so that it slides a distanced down the wall making an angle β with the horizontal, then
Open in App
Solution
The correct option is A a=btanα+β2
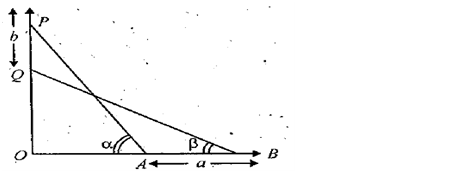 In ΔOQB,cosβ=OBBQ⇒ OB=ℓcosβ...........................(1)Similarly in ΔOPA,cosα=OAPA⇒OA=ℓcosα.........................(2)Nowa=OB–OA=ℓ(cosβ–cosα)..................(3)Also from ΔOAP,OP=ℓsinαAnd in △OQB;OQ=ℓsinβ∴b=OP–OQ=ℓ(sinα–sinβ)......................(4)Dividing eq. (3) by (4) we get
In ΔOQB,cosβ=OBBQ⇒ OB=ℓcosβ...........................(1)Similarly in ΔOPA,cosα=OAPA⇒OA=ℓcosα.........................(2)Nowa=OB–OA=ℓ(cosβ–cosα)..................(3)Also from ΔOAP,OP=ℓsinαAnd in △OQB;OQ=ℓsinβ∴b=OP–OQ=ℓ(sinα–sinβ)......................(4)Dividing eq. (3) by (4) we get
ab=cosβ–cosαsinα–sinβ
=2sinα+β2.sinα−β22cosα+β2.sinα−β2
⇒ ab=tan(α+β)2Thus , a=b tan(α+β)2 is proved

In ΔOQB,cosβ=OBBQ
⇒ OB=ℓcosβ...........................(1)
Similarly in ΔOPA,cosα=OAPA
⇒OA=ℓcosα.........................(2)
Nowa=OB–OA=ℓ(cosβ–cosα)..................(3)
Also from ΔOAP,OP=ℓsinα
And in △OQB;OQ=ℓsinβ
∴b=OP–OQ=ℓ(sinα–sinβ)......................(4)
Dividing eq. (3) by (4) we get
ab=cosβ–cosαsinα–sinβ
=2sinα+β2.sinα−β22cosα+β2.sinα−β2
⇒ ab=tan(α+β)2
Thus , a=b tan(α+β)2 is proved
Suggest Corrections
0
