8
Question
A small mass slides down an inclined plane of inclination with the horizontal. The coefficient friction is where is the distance through which the mass slides down and is a positive constant. Then the distance covered by the mass before it stops is
A small mass slides down an inclined plane of inclination with the horizontal. The coefficient friction is where is the distance through which the mass slides down and is a positive constant. Then the distance covered by the mass before it stops is
Open in App
Solution
Srep1: Given data
- The coefficient of friction is .
- The angle of the inclined plane is .
Diagram
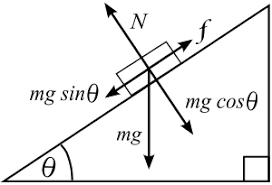
Step2: Frictional force and acceleration
- The frictional force is the force that resists the motion of a body over any surface contact with the body.
- The frictional force is defined by the form, , where, N is the normal force exerted on a body and is the coefficient of friction.
- Acceleration is the time rate of change in velocity. Acceleration is defined as , where, v is the velocity of the body.
Step4: Finding the acceleration
From the figure, it is clear that the normal force exerted on the body is .
As we know, the frictional force is .
So, the equation of the force of the body from the figure is
Step4: Finding the distance
We know the acceleration,
or
Comparing equations 1 and 2 we get,
Integrating equation 3
So, acceleration of the body is
Srep1: Given data
- The coefficient of friction is .
- The angle of the inclined plane is .
Diagram
Step2: Frictional force and acceleration
- The frictional force is the force that resists the motion of a body over any surface contact with the body.
- The frictional force is defined by the form, , where, N is the normal force exerted on a body and is the coefficient of friction.
- Acceleration is the time rate of change in velocity. Acceleration is defined as , where, v is the velocity of the body.
Step4: Finding the acceleration
From the figure, it is clear that the normal force exerted on the body is .
As we know, the frictional force is .
So, the equation of the force of the body from the figure is
Step4: Finding the distance
We know the acceleration,
or
Comparing equations 1 and 2 we get,
Integrating equation 3
So, acceleration of the body is
Suggest Corrections
1
View More
Join BYJU'S Learning Program
Join BYJU'S Learning Program
