1
Question
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60o, Calculate the numerical values of :
(i) ∠ ABD ,
(ii) ∠ DBC,
(iii) ∠ ADC.

AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60o, Calculate the numerical values of :
(i) ∠ ABD ,
(ii) ∠ DBC,
(iii) ∠ ADC.

Open in App
Solution
Join B and D as shown in the diagram.
(i)  (angle subtended by an chord on the center is double that subtended by the same chord on the circumference)
(angle subtended by an chord on the center is double that subtended by the same chord on the circumference)
(ii)  (angle in semi circle)
(angle in semi circle)
Since  is equilateral
is equilateral

Since 
 (alternate angles)
(alternate angles)
(ii) 
 (
( 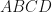 is a cyclic quadrilateral)
is a cyclic quadrilateral)

Join B and D as shown in the diagram.
(i) (angle subtended by an chord on the center is double that subtended by the same chord on the circumference)

(ii) (angle in semi circle)
Since is equilateral
Since
(alternate angles)
(ii)
(
is a cyclic quadrilateral)
Suggest Corrections
6
View More
Join BYJU'S Learning Program
Join BYJU'S Learning Program





