Question

Figure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from its equilibrium position and released, find the period of its vertical oscillation.

• A.
• B. $T=2\pi \sqrt{\frac{3m}{k}}$
• C. $T=2\pi \sqrt{\frac{2m}{k}}$
• D. $T=2\pi \sqrt{\frac{m}{k}}$

Answer 1

The correct option is A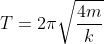

In this case if the mass m moves down a distance from its equilibrium position, then pulley will move down by $\frac{x}{2}$. So, the extra force in spring will be k $\frac{x}{2}$. Now, as the pulley is massless, this force $\frac{kx}{2}$ is equal to extra 2T or T=$\frac{kx}{2}$. This is also the restoring force of the mass.Hence,

or F= - $\frac{kx}{4}$

or a = $-\frac{k}{4m}x$

or T=$2\pi \sqrt{\left|\frac{x}{a}\right|}$

or T= $2\pi \sqrt{\frac{4m}{k}}$