1
Question
Find all the other zeroes of the polynomial p(x)=2x4−7x2+19x2−14x+30 if two zeroes are √2 and −√2
Open in App
Solution
Since the two zeroes of the given polynomial p(x)=2x4+7x3−19x2−14x+30 are √2 and −√2, therefore,
(x−√2)(x+√2)=x2−2 is a factor of the given polynomial.
now, we divide the polynomial p(x)=2x4+7x3−19x2−14x+30 by x2−2 as shown below:
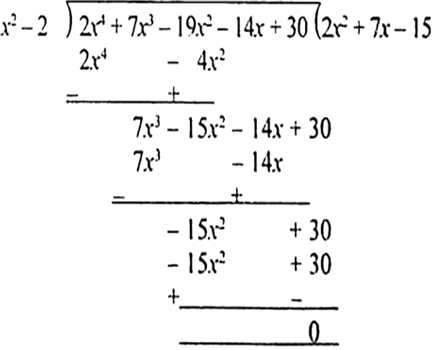
Therefore, 2x4+7x3−19x2−14x+30=(x2−2)(2x2+7x−15)
Now, we factorize 2x2+7x−15 as follows:
2x2+7x−15=0⇒2x2+10x−3x−15=0⇒2x(x+5)−3(x+5)=0⇒(2x−3)(x+5)=0⇒2x−3=0,x+5=0⇒2x=3,x=−5⇒x=32,x=−5
Hence, the zeroes of the polynomial p(x)=2x4+7x3−19x2−14x+30 are √2,−√2,32,−5.
(x−√2)(x+√2)=x2−2 is a factor of the given polynomial.
now, we divide the polynomial p(x)=2x4+7x3−19x2−14x+30 by x2−2 as shown below:
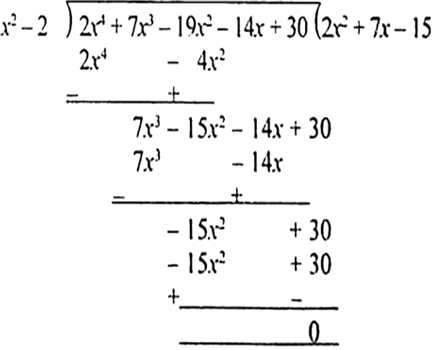
Therefore, 2x4+7x3−19x2−14x+30=(x2−2)(2x2+7x−15)
Now, we factorize 2x2+7x−15 as follows:
2x2+7x−15=0⇒2x2+10x−3x−15=0⇒2x(x+5)−3(x+5)=0⇒(2x−3)(x+5)=0⇒2x−3=0,x+5=0⇒2x=3,x=−5⇒x=32,x=−5
Hence, the zeroes of the polynomial p(x)=2x4+7x3−19x2−14x+30 are √2,−√2,32,−5.
Suggest Corrections
0
