1
Question
If x, y, and z are three-digit positive integers and if x=y+z, is the hundreds digit of x equal to the sum of the hundreds digits of y and z?
(1) The tens digit of x is equal to the sum of the tens digits of y and z.
(2) The units digit of x is equal to the sum of the units digits of y and z.
If x, y, and z are three-digit positive integers and if x=y+z, is the hundreds digit of x equal to the sum of the hundreds digits of y and z?
(1) The tens digit of x is equal to the sum of the tens digits of y and z.
(2) The units digit of x is equal to the sum of the units digits of y and z.
Open in App
Solution
The correct option is B Statement (1) alone is sufficient, but statement (2) alone is not sufficient.
Letting x = 100a + 10b + c, y = 100p + 10q + r, and z = 100t + 10u + v, where a, b, c, p, q, r, t, u, and v are digits, determine if a = p + t. - It is given that b = q + u (which implies that
 because if c + v > 9, then in the addition process a ten would need to be carried over to the tens column and b would be q + u + 1). Since b is a digit,
because if c + v > 9, then in the addition process a ten would need to be carried over to the tens column and b would be q + u + 1). Since b is a digit, 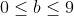 . Hence,
. Hence,  , and so
, and so  . Therefore, in the addition process, there are no hundreds to carry over from the tens column to the hundreds column, so a = p + t; SUFFICIENT.
. Therefore, in the addition process, there are no hundreds to carry over from the tens column to the hundreds column, so a = p + t; SUFFICIENT. - It is given that c = r + v. If x = 687, y = 231, and z = 456, then, y + z = 231 + 456 = 687 = x, r + v = 1 + 6 = 7 = c, and p + t = 2 + 4 = 6 = a. On the other hand, if x = 637, y = 392, and z = 245, then y + z = 392 + 245 = 637 = x, r + v = 2 + 5 = 7 = c, and
 ; NOT sufficient.
; NOT sufficient.
- The correct answer is A; statement 1 alone is sufficient.
Letting x = 100a + 10b + c, y = 100p + 10q + r, and z = 100t + 10u + v, where a, b, c, p, q, r, t, u, and v are digits, determine if a = p + t.
- It is given that b = q + u (which implies that
because if c + v > 9, then in the addition process a ten would need to be carried over to the tens column and b would be q + u + 1). Since b is a digit,
. Hence,
, and so
. Therefore, in the addition process, there are no hundreds to carry over from the tens column to the hundreds column, so a = p + t; SUFFICIENT.
- It is given that c = r + v. If x = 687, y = 231, and z = 456, then, y + z = 231 + 456 = 687 = x, r + v = 1 + 6 = 7 = c, and p + t = 2 + 4 = 6 = a. On the other hand, if x = 637, y = 392, and z = 245, then y + z = 392 + 245 = 637 = x, r + v = 2 + 5 = 7 = c, and
; NOT sufficient.
- The correct answer is A; statement 1 alone is sufficient.
Suggest Corrections
0
View More
Join BYJU'S Learning Program
Join BYJU'S Learning Program
