1
Question
In a rectangle ABCD, P, Q, R and S are the midpoints of the sides AB, BC, CD and DA respectively. Find the area of PQRS in terms of area of ABCD.
Open in App
Solution
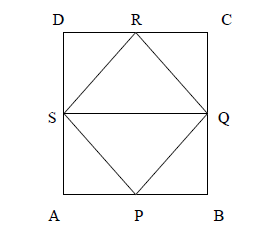
Given: ABCD is a rectangle, P,Q,R and S are the midpoints of AB,BC,CD and DA respectively. PQ,QR,RS and SP are joined.
To find: the areas (PQRS) in terms of area (ABCD)
S and Q are the mid-point of AD and BC.
Therefore, SQ divides rectangles ABCD into two rectangles equal in area.
Area(ABQS)= area(SQCD)=12area(ABCD)
ΔSRQ and parallelogram (rectangles) SQCD stand on the same base SQ and are between the same parallel.
Therefore, AreaΔSRQ=12 area(SQCD)
Similarly AreaΔSPQ=12 area(SABQ)
Adding, area ΔSRQ+ area ΔSPQ=12 area (SQCD)+12 area (SABQ)
i.e., area (PQRS)=12 area (ABCD)
Hence, area (PQRS)=12 area (ABCD).

Given: ABCD is a rectangle, P,Q,R and S are the midpoints of AB,BC,CD and DA respectively. PQ,QR,RS and SP are joined.
To find: the areas (PQRS) in terms of area (ABCD)
S and Q are the mid-point of AD and BC.
Therefore, SQ divides rectangles ABCD into two rectangles equal in area.
Area(ABQS)= area(SQCD)=12area(ABCD)
ΔSRQ and parallelogram (rectangles) SQCD stand on the same base SQ and are between the same parallel.
Therefore, AreaΔSRQ=12 area(SQCD)
Similarly AreaΔSPQ=12 area(SABQ)
Adding, area ΔSRQ+ area ΔSPQ=12 area (SQCD)+12 area (SABQ)
i.e., area (PQRS)=12 area (ABCD)
Hence, area (PQRS)=12 area (ABCD).
Suggest Corrections
0
View More
Join BYJU'S Learning Program
Join BYJU'S Learning Program

