1
Question
In the figure, given below, AD = BC, ∠BAC=30∘ and ∠CBD=70∘.
Find :
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ADB

In the figure, given below, AD = BC, ∠BAC=30∘ and ∠CBD=70∘.
Find :
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ADB

Open in App
Solution
From  ( angles in the same segment)
( angles in the same segment)
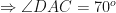
From 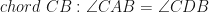 (angles in the same segment)
(angles in the same segment)

In 
Since 
In 
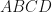 is a cyclic quadrilateral.
is a cyclic quadrilateral. 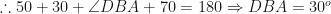
Hence
(i) 
(ii) 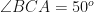
(iii) 
(iv) 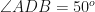

From ( angles in the same segment)
From (angles in the same segment)
In
Since
In
is a cyclic quadrilateral.
Hence
(i)
(ii)
(iii)
(iv)
Suggest Corrections
9
View More
Join BYJU'S Learning Program
Join BYJU'S Learning Program


