1
Question
In the following figure, AB is the diameter of a circle with centre O and CD is the chord with length euqal to radius OA.
If AC produced and BD produced meet at point P; show that : ∠APB=60∘.

In the following figure, AB is the diameter of a circle with centre O and CD is the chord with length euqal to radius OA.
If AC produced and BD produced meet at point P; show that : ∠APB=60∘.

Open in App
Solution
Given: 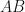 is diameter,
is diameter, 
In 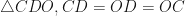
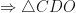 is equilateral
is equilateral
Therefore 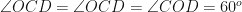
 In
In 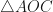
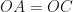 (radius of the same circle)
(radius of the same circle)
Therefore 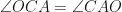
Similarly in 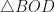
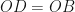 (radius of the same circle)
(radius of the same circle)
Therefore 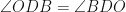
Since 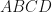 is cyclic quadrilateral
is cyclic quadrilateral
Therefore 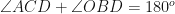 (opposite angles of a cyclic quadrilateral are supplementary)
(opposite angles of a cyclic quadrilateral are supplementary)

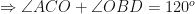
In 

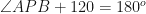
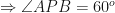 . Hence proved.
. Hence proved.

Given: is diameter,
In
is equilateral
Therefore
 In
In
(radius of the same circle)
Therefore
Similarly in
(radius of the same circle)
Therefore
Since is cyclic quadrilateral
Therefore (opposite angles of a cyclic quadrilateral are supplementary)
In
. Hence proved.
Suggest Corrections
4
View More
Join BYJU'S Learning Program
Join BYJU'S Learning Program


