1
Question
In the given figure, O is the centre of the circle with radius 5 cm. OP and OQ are perpendiculars to AB and CD respectively. AB = 8 cm and CD = 6 cm. Determine the length of PQ.

In the given figure, O is the centre of the circle with radius 5 cm. OP and OQ are perpendiculars to AB and CD respectively. AB = 8 cm and CD = 6 cm. Determine the length of PQ.

Open in App
Solution
Given: 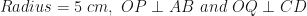
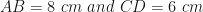
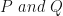 are mid point of
are mid point of 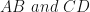 respectively (
respectively (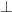 from the center to a chord will bisect the chord)
from the center to a chord will bisect the chord)
 In
In 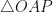
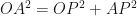
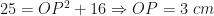
Similarly, in 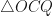

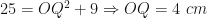
Hence 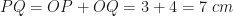

Given:
are mid point of
respectively (
from the center to a chord will bisect the chord)
 In
In
Similarly, in
Hence
Suggest Corrections
10



