1
Question
Let ABCD be a parallelogram. Let BP and DQ be perpendiculars respectively from B and D on to AC. Prove that BP=DQ.
Open in App
Solution
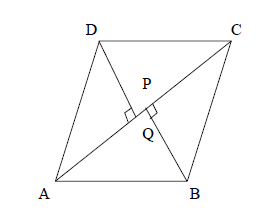
It is given that in parallelogram ABCD, BP is perpendicular to AC and DQ is perpendicular to AC.
In ΔADQ and ΔCBP,
AD=CD (Opposite sides of a parallelogram)
∠DAQ=∠BCP and AD||BC,AC (Transversal alternate angles)
∠DQA=∠BPC=900 (Given)
⸫ΔADQ=ΔCBP (SAA)
⸫BP=DQ (C.P.C.T)
Hence proved.

It is given that in parallelogram ABCD, BP is perpendicular to AC and DQ is perpendicular to AC.
In ΔADQ and ΔCBP,
AD=CD (Opposite sides of a parallelogram)
∠DAQ=∠BCP and AD||BC,AC (Transversal alternate angles)
∠DQA=∠BPC=900 (Given)
⸫ΔADQ=ΔCBP (SAA)
⸫BP=DQ (C.P.C.T)
Hence proved.
Suggest Corrections
0

