You visited us 1 times! Enjoying our articles? Unlock Full Access!

General Solutions of (sin theta)^2 = (sin alpha)^2 , (cos theta)^2 = (cos alpha)^2 , (tan theta)^2 = (tan alpha)^2

Let α, β be a...

Question

Let $α, β$ be any two positive value of x for which 2cosx, |cosx| and 1 - 3 $c o s^{2} x$ are in G.P. The minimum value of $| α - β |$ is

No worries! We‘ve got your back. Try BYJU‘S free classes today!

$\frac{\pi}{6}$

Right on! Give the BNAT exam to get a 100% scholarship for BYJUS courses

Open in App

Solution

The correct option is D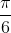
$\frac{\pi}{6}$

$c o s^{2} x = 2 c o s x (1 - 3 c o s^{2} x)$

cosx ${6 c o s^{2} x + c o s x - 2} = 0$

cosx = 0, $\frac{1}{2}, \frac{- 2}{3}$

Thus smallest value of x are $\frac{π}{3}$ and $\frac{π}{2}$

$\Rightarrow | α - β | = \frac{π}{6}$

Suggest Corrections

Similar questions

α

β

x

2 cos x, | cos x |,

1 - 3 {cos}^{2} x

| α - β |

α, β

x

2 cos x, | cos x | a n d 1 - 3 {cos}^{2} x

| α - β |

α

β

2 cos x

| cos x |

1 - 3 {cos}^{2} x

| α - β |

a_{n}

n^{t h}

100 \sum n = 1 a_{2 n} = α

100 \sum n = 1 a_{2 n - 1} = β, α \neq β .

\sum_{n = 1}^{100} a_{2 n} = α and \sum_{n = 1}^{100} a_{2 n - 1} = β,

Join BYJU'S Learning Program