1
Question
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
Open in App
Solution
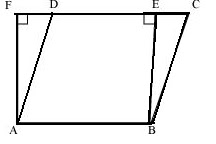
Given: Parallelogram ABCD and rectangle ABEF are on same base and have equal areas.
AB=CD ...opposite side of parallelogram
AB=EF ...opposite side of rectangle
and, ∠F=∠E=90∘
AD>AF and BC>BE ....(Hypotenuse of right angle is greater than other sides )
Now,
Perimeter of □ABCD=AB+BC+CD+DA
Perimeter of □ABEF=AB+BE+EF+FA Since, CD=EF and AD>AF,BC>BE
∴ Perimeter of parallelogram ABCD> Perimeter of rectangle ABEF
Given: Parallelogram ABCD and rectangle ABEF are on same base and have equal areas.
AB=CD ...opposite side of parallelogram
AB=EF ...opposite side of rectangle
and, ∠F=∠E=90∘
AD>AF and BC>BE ....(Hypotenuse of right angle is greater than other sides )
Now,
Perimeter of □ABCD=AB+BC+CD+DA
Perimeter of □ABEF=AB+BE+EF+FA
Since, CD=EF and AD>AF,BC>BE
∴ Perimeter of parallelogram ABCD> Perimeter of rectangle ABEF
Suggest Corrections
1


