1
Question
Prove that if the mid-points of the opposite sides of a quadrilateral are joined, they bisect each other.
Open in App
Solution
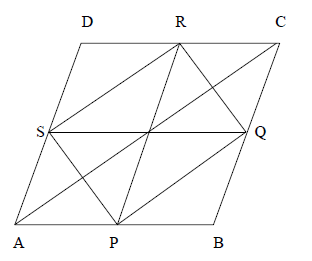
Given: ABCD is a quadrilateral P,Q,R and S are mid-points of AB,BC,CD and DA respectively.
To prove: PR and SQ bisect each other.
Construction: join AC.
In ΔABC,PQ||AC, and PQ=12AC (mid-point theorem) ……. (1)In ΔADC,SR||AC, and SR=12AC (mid-point theorem) ……. (2)
Therefore, PQ||SR and PQ=SR (from (1) and (2) opposite sides equal and parallel)
Thus, PQRS is a parallelogram and PR and SQ are diagonals
Hence, PR bisect SQ.

Given: ABCD is a quadrilateral P,Q,R and S are mid-points of AB,BC,CD and DA respectively.
To prove: PR and SQ bisect each other.
Construction: join AC.
In ΔABC,PQ||AC, and PQ=12AC (mid-point theorem) ……. (1)
In ΔADC,SR||AC, and SR=12AC (mid-point theorem) ……. (2)
Therefore, PQ||SR and PQ=SR (from (1) and (2) opposite sides equal and parallel)
Thus, PQRS is a parallelogram and PR and SQ are diagonals
Hence, PR bisect SQ.
Suggest Corrections
0
