1
Question
Prove the converse of the mid-point theorem following the guidelines given below: Consider a triangle ABC with D as the mid-point of AB. Draw DE∥BC to intersect AC in E. Let E1 be the mid-point of AC. Use mid-point theorem to get DE1∥BC and DE1=BC/2. Conclude E=E1 and hence E is the mid-point of AC.
Open in App
Solution
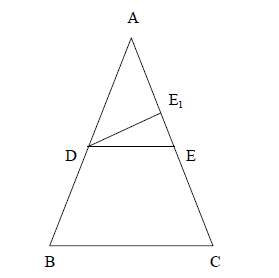
Given: In ΔABC,D is the mid-point of AB.DE||BC
To prove: E is the midpoint of AC
In ΔABC,D is the mid-point of AB.DE||BC (Given)Let E, be the mid-point of AC.
Join DE,D is the mid-point of AB and E1 is the mid-point of AC.
∴DE1||BC (Mid-point theorem parallels)But DE||BC (Given)
This is possible only if E and E1 consider (Through a given point, only one line can be drawn || to be a given line)
Therefore, E and E1 coincide.
i.e. DE1 is the same as DE.
Thus a line drawn through the mid-point of a side of a triangle and parallel to another bisects the third side.
Hence, E=E1 and E is the mid-point of AC.

Given: In ΔABC,D is the mid-point of AB.DE||BC
To prove: E is the midpoint of AC
In ΔABC,D is the mid-point of AB.DE||BC (Given)
Let E, be the mid-point of AC.
Join DE,D is the mid-point of AB and E1 is the mid-point of AC.
∴DE1||BC (Mid-point theorem parallels)
But DE||BC (Given)
This is possible only if E and E1 consider (Through a given point, only one line can be drawn || to be a given line)
Therefore, E and E1 coincide.
i.e. DE1 is the same as DE.
Thus a line drawn through the mid-point of a side of a triangle and parallel to another bisects the third side.
Hence, E=E1 and E is the mid-point of AC.
Suggest Corrections
0
View More
Join BYJU'S Learning Program
Join BYJU'S Learning Program



