3
Question
The figure shown a circle with centre O AB is the side of regular pentagon and AC is the side of regular hexagon.
Find the angles of triangle ABC.

The figure shown a circle with centre O AB is the side of regular pentagon and AC is the side of regular hexagon.
Find the angles of triangle ABC.

Open in App
Solution
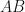 is the side of a regular pentagon
is the side of a regular pentagon
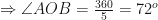

 is a side of regular hexagon
is a side of regular hexagon
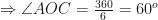
Now 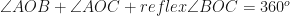
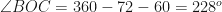
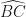 subtends
subtends 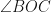 at the center and
at the center and  on the circumference
on the circumference
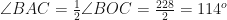
Similarly 
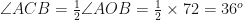
Therefore 

is the side of a regular pentagon

is a side of regular hexagon
Now
subtends
at the center and
on the circumference
Similarly
Therefore
Suggest Corrections
5
View More
Join BYJU'S Learning Program
Join BYJU'S Learning Program




