1
Question
The internal and external diameter of a hollow hemispherical shell are 6 cm and 10 cm respectively. What is the total surface area of the shell?
The internal and external diameter of a hollow hemispherical shell are 6 cm and 10 cm respectively. What is the total surface area of the shell?
Open in App
Solution
The correct option is B 84π cm2
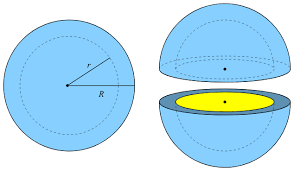
Observe from the figure that the total surface area of a hemispherical shell is the sum of the inner curved surface area, outer curved surface area and the area of the ring.
Given, inner diameter of the shell = 6 cm
So, inner radius(r) = 3 cm
Therefore, inner curved surface area of the shell
= 2πr2
= 2π×32
= 18π cm2
Given, outer diameter of the shell = 10 cm
So, outer radius of the shell(R) = 5 cm
Therefore, outer curved surface area of the shell
= 2πR2
= 2π×52
= 50π cm2
Now, inner radius of the ring is 3 cm and outer radius of the ring is 5 cm.
Therefore, area of the ring
= π(R2−r2)
= π(52−32)
= 16π cm2
∴ Total surface area = Inner curved surface area + Outer curved surface area + Area of the ring
= 50π cm2 + 18π cm2 + 16π cm2
= 84π cm2
Observe from the figure that the total surface area of a hemispherical shell is the sum of the inner curved surface area, outer curved surface area and the area of the ring.
Given, inner diameter of the shell = 6 cm
So, inner radius(r) = 3 cm
Therefore, inner curved surface area of the shell
= 2πr2
= 2π×32
= 18π cm2
Given, outer diameter of the shell = 10 cm
So, outer radius of the shell(R) = 5 cm
Therefore, outer curved surface area of the shell
= 2πR2
= 2π×52
= 50π cm2
Now, inner radius of the ring is 3 cm and outer radius of the ring is 5 cm.
Therefore, area of the ring
= π(R2−r2)
= π(52−32)
= 16π cm2
∴ Total surface area = Inner curved surface area + Outer curved surface area + Area of the ring
= 50π cm2 + 18π cm2 + 16π cm2
= 84π cm2
Suggest Corrections
0
Join BYJU'S Learning Program
Join BYJU'S Learning Program
