is a rectangle in which diagonal bisects as well as. Show that:
- is a square.
- Diagonal bisects as well as .
is a rectangle in which diagonal bisects as well as. Show that:
- is a square.
- Diagonal bisects as well as .
Step Drawing the diagram:
is a rectangle in which diagonal bisects as well as.
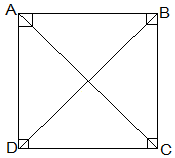
Join diagonal .
Step Proving is a square:
As, diagonal bisects as well as,
As we know that every rectangle is a parallelogram.
is a parallelogram.
[ Alternate interior angles are equal]
From and , we have
In ,
then,
[Sides opposite to equal angles of a triangle are equal]
Similarly,
In, rectangle
(opposite sides of rectangle are equal)
Therefore, is a square.
Step Proving Diagonal bisects as well as :
In ,
(Side of square)
(Angles opposite to equal sides are equal)
In ,
(Side of square)
(Angles opposite to equal sides are equal)
And, [ Alternate interior angles are equal]
Therefore, Diagonal bisects as well as .
Hence proved.
Step Drawing the diagram:
is a rectangle in which diagonal bisects as well as.

Join diagonal .
Step Proving is a square:
As, diagonal bisects as well as,
As we know that every rectangle is a parallelogram.
is a parallelogram.
[ Alternate interior angles are equal]
From and , we have
In ,
then,
[Sides opposite to equal angles of a triangle are equal]
Similarly,
In, rectangle
(opposite sides of rectangle are equal)
Therefore, is a square.
Step Proving Diagonal bisects as well as :
In ,
(Side of square)
(Angles opposite to equal sides are equal)
In ,
(Side of square)
(Angles opposite to equal sides are equal)
And, [ Alternate interior angles are equal]
Therefore, Diagonal bisects as well as .
Hence proved.
