1
Question
An open cylindrical vessel of internal diameter 7 cm and height 8 cm stands on a horizontal table. Inside this is placed a solid metallic right circular cone, the diameter of whose base is 312 cm and height 8 cm. Find the volume of water required to fill the vessel. If this cone is replaced by another cone, whose height is 134 cm and the radius of whose base is 2 cm, find the drop in the water level.
An open cylindrical vessel of internal diameter 7 cm and height 8 cm stands on a horizontal table. Inside this is placed a solid metallic right circular cone, the diameter of whose base is 312 cm and height 8 cm. Find the volume of water required to fill the vessel. If this cone is replaced by another cone, whose height is 134 cm and the radius of whose base is 2 cm, find the drop in the water level.
Open in App
Solution
Cylinder: 
Cone: 
Volume of water required 

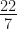



If the cone was replaced by another cone with 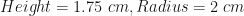 , then let the drop in water level
, then let the drop in water level  . Therefore
. Therefore
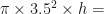

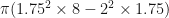
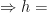



Cylinder:
Cone:
Volume of water required
If the cone was replaced by another cone with , then let the drop in water level
. Therefore
Suggest Corrections
3
View More
Join BYJU'S Learning Program
Join BYJU'S Learning Program
