The heavier block is an Atwood machine that has a mass twice that of the lighter one. The tension in the string is when the system is set into motion. Find the decrease in the gravitational potential energy during the first second after the system is released from rest?
The heavier block is an Atwood machine that has a mass twice that of the lighter one. The tension in the string is when the system is set into motion. Find the decrease in the gravitational potential energy during the first second after the system is released from rest?
Step 1: Given data:
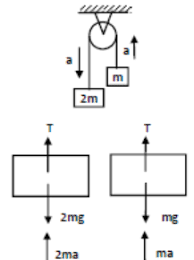
Given that,
Tension
Step 2: Formula for calculating the decreased potential energy:
The formula for the decreased potential energy can be given as
Step 3: Expression for the equation of motion:
The equation of motion is basically the equations used to derive components such as displacement(s), velocity (initial and final), time(t) and acceleration(a), which can be given as:
Where, displacement, velocity, time, and acceleration
The above equation of motion is called the second equation of motion.
Step 4: Calculating the value of :
We know,
From equation
Now, put the value of g in the equation
Now, from the equation of motion
At
Thus, a change in the height of the block will be;
Step 4: calculating the value of the decreased potential energy :
Now, decrease potential energy can be calculated as:
Hence, the decreased gravitational potential energy is .
Step 1: Given data:
Given that,
Tension
Step 2: Formula for calculating the decreased potential energy:
The formula for the decreased potential energy can be given as
Step 3: Expression for the equation of motion:
The equation of motion is basically the equations used to derive components such as displacement(s), velocity (initial and final), time(t) and acceleration(a), which can be given as:
Where, displacement, velocity, time, and acceleration
The above equation of motion is called the second equation of motion.
Step 4: Calculating the value of :
We know,
From equation
Now, put the value of g in the equation
Now, from the equation of motion
At
Thus, a change in the height of the block will be;
Step 4: calculating the value of the decreased potential energy :
Now, decrease potential energy can be calculated as:
Hence, the decreased gravitational potential energy is .
