1
Question
A solid sphere of mass , radius, and having a moment of inertia about an axis passing through the center of mass as is recast into a disc of thickness , whose moment of inertia about an axis passing through its edge and perpendicular to its plane remains . Then, the radius of the disc will be
A solid sphere of mass , radius, and having a moment of inertia about an axis passing through the center of mass as is recast into a disc of thickness , whose moment of inertia about an axis passing through its edge and perpendicular to its plane remains . Then, the radius of the disc will be
Open in App
Solution
Step 1: Given data
The mass of the sphere is .
The radius of the sphere is .
The moment of inertia of the sphere is
The moment of inertia of the disc is .
Step 2: Moment of inertia
- The moment of inertia of a body about a given axis in space is the sum of the products of the mass and square of the distance from the axis for each particle comprising the body.
- The moment of inertia is defined by the form, , where, m is the mass of the body and x is the distance of the body from the axis of rotation.
Step 3: Moment of inertia of a solid sphere and a disc.
- The moment of inertia of a sphere about an axis passing through the diameter is , where, m is the mass of the sphere and r is the radius of the solid sphere.
- The moment of inertia of a disc about an axis passing through its edge and perpendicular to its plane is , where, m is the mass of the sphere and r is the radius of the solid sphere.
Step 4: Diagram
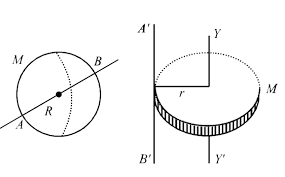
Step 5: Finding the radius of the disc
According to the question, in both cases, the moment of inertia is the same, i.e, .
So,
Therefore, the radius of the disc is .
Step 1: Given data
The mass of the sphere is .
The radius of the sphere is .
The moment of inertia of the sphere is
The moment of inertia of the disc is .
Step 2: Moment of inertia
- The moment of inertia of a body about a given axis in space is the sum of the products of the mass and square of the distance from the axis for each particle comprising the body.
- The moment of inertia is defined by the form, , where, m is the mass of the body and x is the distance of the body from the axis of rotation.
Step 3: Moment of inertia of a solid sphere and a disc.
- The moment of inertia of a sphere about an axis passing through the diameter is , where, m is the mass of the sphere and r is the radius of the solid sphere.
- The moment of inertia of a disc about an axis passing through its edge and perpendicular to its plane is , where, m is the mass of the sphere and r is the radius of the solid sphere.
Step 4: Diagram
Step 5: Finding the radius of the disc
According to the question, in both cases, the moment of inertia is the same, i.e, .
So,
Therefore, the radius of the disc is .
Suggest Corrections
1
View More
Join BYJU'S Learning Program
Join BYJU'S Learning Program
