SEBA Board Class 9 Maths syllabus is prescribed by the Board of Secondary Education. Mathematics syllabus is designed according to the psychological acceptance level of students without compromising the quality. Students are given ample exercise problems and assignments for consistent practice and better understanding. SEBA Board Class 9 Maths syllabus comprises principal area of proofs in mathematics and mathematical modeling. That includes – Number Systems, Algebra, Coordinate Geometry, Geometry, Mensuration, Statistics and Probability.
This year, the SEBA syllabus was reduced due to the Covid-19 pandemic. Click the link given below to download FREE PDF of the revised Mathematics syllabus of SEBA Board Class 9:
Download SEBA Board Class 9 Maths Reduced syllabus PDF 2021-22
Mathematics is called the ‘Queen of the Sciences’. Because the moment we wake up until we go to bed each and every activity involves calculations. That is Mathematics embedded in our daily routine without our knowledge. Students often find mathematics as a hard bite.
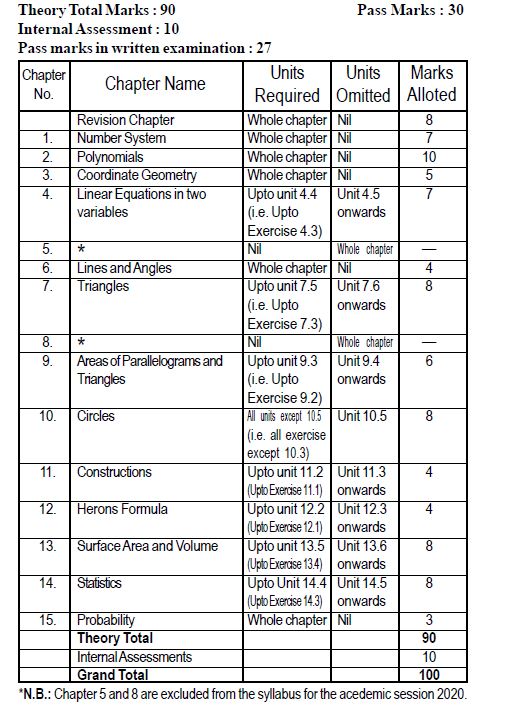
Refer the table given below for detailed syllabus of SEBA Board Class 9:
(The screenshot from the syllabus 2020 is given below, as it contains the same units for this year as well).
Learn Maths & Science in an interactive & fun-loving way with BYJU’S App/Tablet
Comments