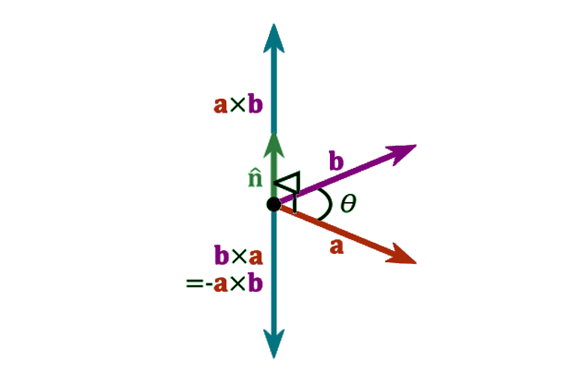
Cross Product is given by,\[\LARGE A\times B=\begin{vmatrix} i & j & k\\ a_{1} & a_{2}& a_{3} \\ b_{1} & b_{2}& b_{3} \end{vmatrix}\]
Cross Product Formula is given by,
\[\LARGE a\times b=\left | a \right |\left | b \right |\sin \theta\]
Cross product formula is used to determine the cross product or angle between any two vectors based on the given problem.
Solved Examples
Question 1:Calculate the cross products of vectors a = <3, 4, 7> and b = <4, 9, 2>.
Solution:
The cross product is given by
aÂ
aÂ
a
aÂ
Question 2:
Find the angle between two vector a and b, where a =<-4, 3, 0> and b =<2, 0, 0>
Solution:
We know that, the formula to find the angle between two vectors is
Sin θ = a × b / |a| |b|
Therefore, θ = sin-1[a × b / |a| |b|]
Now, we have to find the cross product of two vectors and b:
= i (0) -j(0) +k(-6)
a × b = -6k
While finding the angle between two vectors, substitute the magnitude of the vector value, Thus,
|a × b| = 6
Therefore,  θ = sin-1[|a × b|/ |a| |b|]
θ = sin-1[ 6/ 5 .2 ]
θ = sin-1[ 3/ 5 ] = 36.87°
Hence, the angle between two vectors, a and b (θ) is 36.87°
To learn more problems, keep visiting BYJU’S – The Learning App and download the app to learn with ease.
Comments