What is Escape Velocity?
Escape velocity is the minimum velocity required by a body to be projected to overcome the gravitational pull of the earth. It is the minimum velocity required by an object to escape the gravitational field that is, escape the land without ever falling back. An object that has this velocity at the earth’s surface will totally escape the earth’s gravitational field ignoring the losses due to the atmosphere.
For example, a spacecraft leaving the surface of Earth needs to go at 7 miles per second, or around 25,000 miles per hour to leave without falling back to the surface.
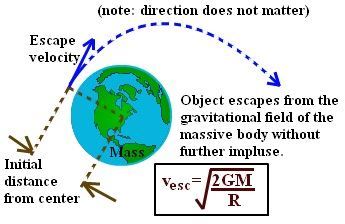
Formula of Escape Velocity
Escape velocity formula is given
Where,
- V is the escape velocity
- G is the gravitational constant is 6.67408 × 10-11 m3 kg-1 s-2
- M is the mass of the planet
- R is the radius from the center of gravity
An alternative expression for the escape velocity particularly useful at the surface on the body is
Where g is the acceleration due to the gravity of earth.
Hence, Escape velocity is also given by
It is expressed in m/s and the escape velocity of earth is 11,200 m/s.
The escape velocity formula is applied in finding the escape velocity of any body or any planet if mass and radius are known.
Solved Examples
Example 1
Determine the escape velocity of the Jupiter if its radius is 7149 Km and mass is 1.898 × Kg
Solution:
Given: Mass M = 1.898 × Kg,
Radius R = 7149 Km
Gravitational Constant G = 6.67408 × 10-11 m3 kg-1 s-2
Escape Velocity is given as
Vesc = √2GM / R
=√2 x 6.67408 × 10-11 x 1.898 × / 7149
50.3 km/s
Example 2
Determine the escape velocity of the moon if Mass is 7.35 × 1022 Kg and the radius is 1.5 × m.
Solution:
Given
M = 7.35 × 1022 Kg,
R = 1.5 × 106 m
Escape Velocity formula is given by
Vesc = √2GMR
= √2×6.673××7.35×1022 / 1.5×
= 7.59 × m/s
This solution of escape speed was proved to be very helpful for me because I was having that doubt but it have cleared my doubt also thanks for solved example I have practice it and now I think I have clear my concept. Thank you